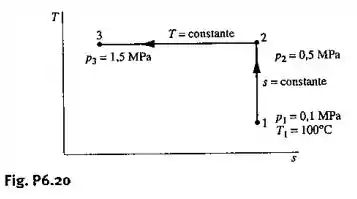
Um quilograma de água contida em um conjunto cilindro-pistão passa por dois processos internamente reversíveis em série ilustrados na Fig. P6.20. Para cada processo, determine o trabalho e a quantidade de transferência de calor, ambos em .
Passo 1
Fala galerinha!
Bora resolver mais uma questão juntos!
Começos o nosso problema analisando o processo , um processo isentrópico.
Sendo um processo isentrópico significa que ele é reversível e adiabático, portanto, a transferência de calor é zero.
Aplicando a Lei da Termodinâmica ao processo :
Pela tabela de propriedades da água satura, a , devemos obter:
Temos que a temperatura fornecida é maior do que a temperatura de saturação em , portanto, o estado 1 está na região superaquecida.
Obtendo as seguintes propriedades na tabela de vapor d’água superaquecido a e :
Como o processo é um processo isentrópico:
Obtendo as propriedades a e na tabela de vapor d’água superaquecido por interpolação:
Substituindo os dados na nossa equação de trabalho:
Vamos para a segunda parte do nosso sistema!
Passo 2
Agora, devemos escrever a equação para a transferência de calor durante o processo da seguinte forma:
Obtendo as propriedades em e na tabela de propriedades do vapor de água superaquecido por interpolação:
Substituindo os dados na nossa equação de transferência de calor:
Calculando o trabalho durante o processo :
Substituindo os dados:
E assim a gente finaliza o nosso exercício!
Até o próximo!