Um sistema que consiste em ar inicialmente de e experimenta os dois tipos de interação descritos a seguir. Em cada caso, o sistema é levado do estado inicial até um em que a temperatura é de , enquanto o volume permanece constante.
a) O aumento da temperatura é realizado adiabaticamente através da agitação do ar por meio de um agitador. Determine a quantidade de entropia gerada, em .
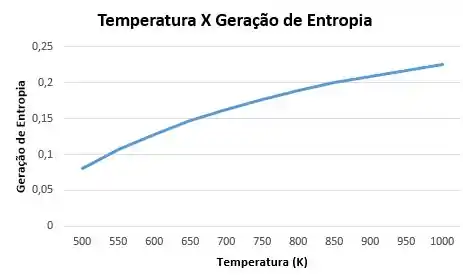
b) O aumento da temperatura é realizado através da transferência de calor de um reservatório à temperatura . A temperatura na fronteira do sistema em que a transferência de calor acontece é também . Represente graficamente a quantidade de entropia gerada, em , em função de para .
Passo 1
Opa, bora resolver essa questão juntos!
Começamos o nosso problema calculando a geração de entropia do ar.
Da tabela com as propriedades do ar como gás ideal, obtemos:
- :
- :
Assim:
Substituindo os dados:
Passo 2
Letra a)
Determinando a quantidade de entropia gerada quando o aumento da temperatura é realizado adiabaticamente:
Como não temos troca de calor:
Assim:
Passo 3
Letra b)
Da equação de equilíbrio de entropia:
Da equação do balanço de energia:
Sem a presença de trabalho:
Obtendo os valores de energia interna específica na tabela utilizada no Passo 1:
- :
- :
Assim:
Substituindo na equação de equilíbrio de entropia:
Para :
Passo 4
Gráfico para , utilizando a equação: