Condução de Energia por Calor
Teoria
O que é condução de energia por calor?
Pra cozinhar, a gente coloca a superfície externa da panela em contato com o fogo, certo? Mas se estamos esquentando apenas o lado de fora da panela com as chamas, como essa energia consegue chegar no interior do recipiente pra esquentar os ingredientes?
Pra entender melhor esse processo, imagina que somos capazes de enxergar o movimento dos átomos que formam a panela.
Isso mesmo! Agora vamos focar nossa supervisão pro lado quente que está em contato direto com o fogo. Veríamos que as moléculas estão bem agitadas por causa da energia que recebem das chamas.
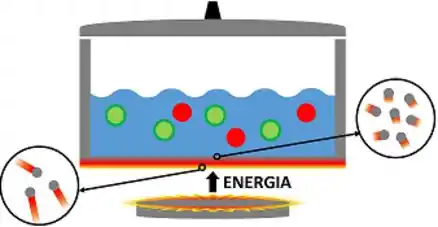
Essa vibração mais forte faz elas colidirem com os átomos próximos que estavam mais “paradões”. Esse impacto faz eles se agitarem mais também. Pra visualizar melhor, é só lembrar do que acontece quando jogamos sinuca.
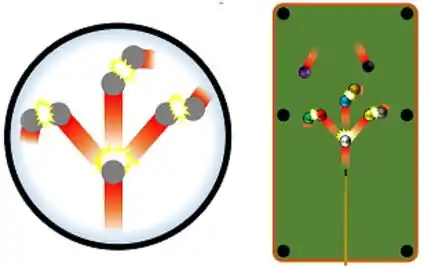
Essas partículas recém estimuladas se chocam com outras, gerando um efeito em cadeia de propagação de movimento. Depois de um tempo, essa movimentação alcança os átomos da superfície interna da panela, o que faz esquentar a comida. Essa transferência de energia molécula a molécula é conhecida como condução de energia por calor.
Quais fatores influenciam a condução?
Agora que já conhecemos a física por trás do processo, dá pra entender melhor quais fatores influenciam a velocidade desse tipo de transmissão de energia. De todos os parâmetros que podemos imaginar, só três têm importância pra gente:
- A área da superfície, onde acontece a transferência de energia
- A diferença de temperatura entre as partes mais quente e mais fria do material
- A capacidade de conduzir energia por calor do material
A diferença de temperatura e a capacidade de conduzir energia por calor aparecem com nomes diferentes em exercícios de condução.
Relaxa, porque a influência de cada uma dessas três variáveis será explicada com mais detalhes já já! Antes, será mostrada a fórmula que calcula a condução de energia por calor!
Lei de Fourier
Essa quantidade de informações pode te fazer pensar que existem equações complicadíssimas pra calcular a velocidade de transferência de energia por condução, mas não se assuste! Todos esses detalhes são resumidos em uma única fórmula chamada lei de Fourier.
onde:
- é a derivada da quantidade de energia transferida por condução em relação ao tempo. Geralmente seu valor está em watt (), mas em exercícios de termodinâmica é comum ver a unidade em quilowatt ().
- é a condutividade térmica do material que compõe o objeto. Por exemplo: no caso da panela, o material é o aço inox. Então teria valor igual à condutividade do aço.
- é a área da superfície onde ocorre a transferência de energia. Tenha cuidado! Seu valor na fórmula deve estar sempre em metro quadrado ().
- é a derivada da temperatura em relação a uma direção . Também pode ser chamada de gradiente de temperatura. Essa derivada representa a contribuição da diferença da temperatura pra velocidade de transferência de energia . Sua unidade segue o Sistema Internacional de Unidades, ou seja: kelvin por metro . Ela também pode estar numa unidade equivalente de grau Celsius por metro .
- As barras laterais da fórmula indicam que estamos calculando apenas o módulo da transferência de energia.
e
Agora vamos ver os efeitos desses fatores na velocidade da condução de energia por calor!
Área da superfície de troca de energia
Pra entender melhor a importância desse fator, vamos retomar o exemplo sobre cozinhar. Dentro desse caso, ao invés de se perguntar como o tamanho da superfície varia a velocidade da condução de energia por calor, vamos descobrir porque a maior boca do fogão esquenta a comida mais rápido. As duas questões têm a mesma resposta!
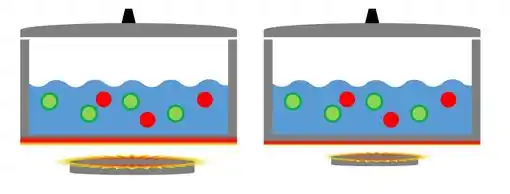
Isso faz muito sentido com o que já aprendemos sobre condução! Olha só: quanto maior a boca do fogão, maior a área de contato entre o fogo e a panela. Isso significa que mais átomos da superfície externa começam a se agitar e a propagar seu movimento até o interior do recipiente. O resultado disso é que mais moléculas do lado de dentro se agitam e conseguem de aquecer a comida. Desse jeito ela esquenta mais rápido!
Diferença de temperatura
Vamos seguir com o exemplo da panela esquentando. No início do aquecimento dela, quando sua temperatura ainda não está muito alta, encostar a mão na sua lateral não é tão perigoso. Nosso corpo não esquenta tão rápido com esse toque. Mas depois de algum tempo com a panela no fogo, um segundo de contato com o metal já é o suficiente pra gente nunca mais querer fazer o teste!
Dessa vez, a energia passa mais rápido para a nossa pele por causa do aumento de temperatura do objeto. Falando isso de outro jeito: a diferença de temperatura entre a parte mais quente (panela) e a parte mais fria (nossa mão) influencia a velocidade do processo.
onde:
- Atenção! Esse pontinho em cima de sempre indica derivação no tempo! Essa regra se aplica para qualquer variável que tenha essa bolinha em cima! Traduzindo, representa a velocidade da troca de energia.
- é a diferença de temperatura entre a parte mais quente e a mais fria.
Condutividade térmica
Por último, já perceberam que segurar uma panela quente toda de metal, esquenta bem mais rápido a mão, do que segurar uma frigideira pelo seu cabo de plástico? Por que isso acontece se a temperatura da chama que aquece os dois é a mesma?
Isso ocorre porque materiais diferentes possuem capacidades diferentes de conduzir energia por calor. Essa característica é chamada de condutividade térmica do material . Quanto maior seu valor, melhor condutor ele é.
Essa variável é representada por nas questões de condução. Sua unidade, nestes exercícios, está de acordo com o Sistema Internacional de Unidades (S.I.):
Ela é lida como watt por metro Kelvin.
Mas fique atento! Em vários problemas a unidade da condutividade térmica é:
onde significa quilowatt.
Outra dica importante pra você: as unidades e são equivalentes entre si. Por isso, as unidades e também se equivalem.
Eixo da lei de Fourier
Quase todos os parâmetros da lei de Fourier já foram bem definidos, mas para entender melhor a derivada da temperatura em relação ao eixo , a gente precisa entender qual direção essa reta representa. Antes, é necessário dizer que em exercícios de condução de energia por calor, a temperatura só varia em uma única direção! Uhul!
E no fim das contas, o eixo é justamente essa direção, na qual a temperatura varia!
Vamos visualizar isso de novo pelo exemplo da panela no fogo. Nesse caso, ela tem uma temperatura maior onde as chamas estão em contato com o metal (superfície de fora). No entanto, esse valor vai caindo para pontos cada vez mais pertos da parte de dentro. Então o eixo é igual ao mostrado pela figura.
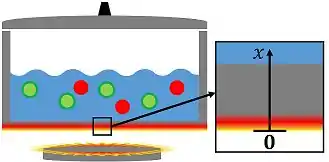
Ele está apontando de fora pra dentro da panela, mas o seu sentido não importa. Isso só interfere no sinal da derivada e ele será desprezado depois, porque estamos calculando apenas o módulo da taxa de transferência de energia.
Depois disso, se quiser saber o sentido da condução de energia, é só lembrar que ela é transmitida do ponto mais quente para o ponto mais frio!
Cálculo da derivada da temperatura
Ok! Essa simplificação ajudou bastante nossa vida! Mas ainda não resolveu todo nosso problema, não é mesmo? A gente já sabe que a temperatura varia em uma direção, mas não sabemos como ela varia nessa direção. A variação é linear? É exponencial? A gente precisa descobrir isso para calcular essa derivada!
Agora pode voltar a sorrir, porque lá vem outra simplificação muito comum nos exercícios de condução: eles consideram a variação da temperatura linear. Aí é só encontrar a inclinação dessa reta para calcular a derivada.
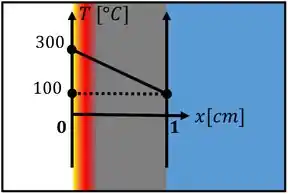
Pra treinar isso, vamos supor que a temperatura da face externa da panela mede e a temperatura do lado interno vale . Por fim, considere que a espessura da sua base é de .
O primeiro passo para resolver a derivada é lembrar de transformar a unidade da espessura de centímetro para metro. Copiando a orientação do eixo indicada na figura:
Com essa dica final, estamos prontos para partirmos pros exercícios.
Quais fatores influenciam a condução?
Lei de Fourier
Área da superfície de troca de energia A
Diferença de temperatura d T d x
Condutividade térmica k
Eixo x da lei de Fourier
Cálculo da derivada da temperatura d T d x
Exercícios Resolvidos
Exercício Resolvido #1
Michael A. Boles e Yunus A. Çengel, Termodinâmica, 5ª ed. New York: McGraw-Hill Education, 2004, pp. 85-2.81C
Qual é o melhor condutor de calor, o diamante ou a prata? Use a tabela abaixo.
Passo 1
O enunciado pede que a gente determine qual é o melhor condutor de calor a partir das informações dadas na tabela. Mas o que é essa variável que aparece na tabela e o que ela tem a ver com condução de calor? Responder isso é a única etapa pra resolver a questão.
O presente na tabela é chamado de condutividade térmica. Esse é só um nome difícil dado para a capacidade que um material tem de conduzir calor. Ou seja, quanto maior o valor da condutividade do material, melhor ele conduz calor! Sua unidade no Sistema Internacional (S.I.) é o watt por metro por kelvin . Então vamos comparar a condutividade do diamante e da prata pra terminar logo esse exercício.
Passo 2
O valor da condutividade térmica do diamante é igual a:
Já o valor da condutividade térmica da prata é igual a:
Ou seja, a condutividade térmica do diamante é maior.
Logo, o diamante conduz melhor o calor.
Resposta
O diamante.
Exercício Resolvido #2
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 90-4.17
Uma placa de compensado apresenta espessura igual . Sabendo que a diferença entre as temperaturas das superfícies expostas da placa é , determine a razão entre taxa de transferência de calor por condução da placa e a área de troca de energia.
Passo 1
O exercício pede para determinar a razão entre taxa de transferência de calor por condução da placa e a área de troca de energia. Mas o que a taxa de transferência de calor por condução significa? Para entender melhor o que esses termo significa, podemos ilustrar o problema.
A taxa de transferência de calor é o nome comum, que os exercícios dão, para a derivada da energia que é transferida através da parede em relação ao tempo.
Para achar esse valor, temos que lembrar a fórmula de condução responsável pelo seu cálculo: a lei de Fourier.
Por essa equação, podemos ver que para encontrar a taxa de calor que atravessa a parede , precisamos primeiro achar o valor de três variáveis:
- A condutividade térmica
- A área onde a energia é trocada
- A derivada da temperatura em relação ao eixo
No entanto, a questão não pede o valor dessa taxa de transferência , mas sim a divisão de por . Ou seja, precisamos rearranjar a lei de Fourier, passando a área para o outro lado da equação, para calcular o que o problema quer. Faremos isso no próximo passo.
Passo 2
Reorganizando a lei de Fourier:
Agora vemos que, para obter o que se pede, não precisamos mais encontrar a área, porque o resultado da divisão só depende da derivada e da condutividade térmica.
Para chegar na resposta, temos que ler o enunciado com atenção, porque ele tem dois tipos de informação: as informações claras, que sabemos como usar, e os dados que ainda precisamos descobrir como usar na fórmula.
Vamos começar pelas informações mais claras:
- O enunciado diz que a condutividade térmica da placa de compensado vale .
- A função das outras duas informações ainda não está claramente definida. São elas:
- , a diferença de temperatura entre as duas superfície da placa
- , a espessura da placa
A primeira variável , fundamental para achar , já está determinada. Mas como calcular ?
Para essa tarefa, precisamos lembrar da simplificação mais comum desses exercícios:
- A temperatura varia linearmente com o eixo .
Passo 3
O eixo é a única direção, em que a temperatura da placa varia. No caso estudado, a diferença de temperatura entre as superfícies é a mesma. Ou seja, a temperatura só muda, conforme variamos a distância do ponto em relação a uma das superfícies.
Vamos representar a variação linear da temperatura para facilitar o cálculo da sua derivada.
No fim, a derivada é igual à inclinação dessa reta!
Passo 4
Agora vamos calcular essa inclinação para determinar . Lembre-se de passar as unidades para o Sistema Internacional de Unidades (SI). Temos então que converter a espessura de milímetro para metro, antes de colocá-la na fórmula.
Passo 5
Essa etapa é só a substituição das duas variáveis na lei de Fourier rearranjada:
Resposta
Exercício Resolvido #3
Michael A. Boles e Yunus A. Çengel, Thermodynamics: An Engineering Approach, 8ª ed. New York: McGraw-Hill Education, 2015, pp. 103-2.91
As superfícies interna e externa de uma parede de tijolos x de de espessura e condutibilidade térmica igual a são mantidas a temperaura de e respectivamente. Determine a taxa de calor transferido através da parede em .
Passo 1
O exercício pede para determinar a taxa de calor que atravessa a parede. Mas o que exatamente isso significa? Vamos ilustrar o problema para facilitar o nosso entendimento.
A taxa de calor é o nome comum, que os exercícios dão para a derivada da energia que é transferida através da parede por condução em relação ao tempo.
Para achar esse valor, temos que lembrar a fórmula de condução responsável pelo seu cálculo: a lei de Fourier.
Por essa equação, podemos ver que para encontrar a taxa de calor que atravessa a parede precisamos primeiro achar o valor de três variáveis:
- A condutibilidade térmica
- A área onde a energia é trocada
- A derivada da temperatura em relação ao eixo ,
Para fazer isso, a gente precisa extrair dois tipos de informação presentes no enunciado: as informações claras e objetivas e os dados que estão escondidos e temos que interpretar nas entrelinhas. Vamos fazer essa identificação no próximo passo.
Passo 2
Vamos começar pelas informações mais claras:
- O enunciado diz que a condutibilidade térmica da parede formada por tijolos vale . Lembre-se que as unidades e são equivalentes. Logo, podemos usar esse valor na fórmula sem precisar converter.
- O valor da área também pode ser calculado rapidamente, mas ele não é informado diretamente como o . O tamanho da superfície de troca é mostrado, quando o enunciado diz as dimensões x da parede. Ou seja:
- A função das outras três informações ainda não está claramente definida. São elas:
- , a temperatura de uma superfície da parede
- , a temperatura da outra superfície da parede
- , a espessura da parede
- A direção do eixo
- Saber como a temperatura varia nesse eixo
As duas primeiras variáveis e , fundamentais para achar , já estão determinadas. Mas como calcular ?
Para essa tarefa, precisamos de dois dados que estão escondidos no enunciado:
Passo 3
O eixo é a única direção, em que a temperatura da parede varia. Mas como sabemos que essa simplificação de variação unidirecional da temperatura está sendo usada nesse caso?
Descobrimos isso, quando a questão diz que cada superfície da parede tem apenas uma temperatura. Uma superfície está a e outra a .
Ou seja, a temperatura de um ponto não varia dentro de uma mesma superfície. Ela só muda, quando a distância entre o ponto considerado e uma das superfície se altera.
Como essa distância só muda conforme caminhamos em uma direção perpendicular às superfícies, o eixo é uma reta perpendicular às superfícies.
Falta agora saber como a temperatura varia ao longo da direção . A única pista do enunciado são as duas temperaturas que ele fornece.
A única função, que pode ser totalmente definida com dois pontos, é uma reta. Por isso, deduzimos que a questão está considerando uma distribuição linear para a temperatura.
No fim, a derivada é igual à inclinação dessa reta!
Passo 4
Agora vamos calcular essa inclinação para determinar . Lembre-se de passar as unidades para o Sistema Internacional de Unidades (SI). Temos então que converter a espessura de centímetro para metro, antes de colocá-la na fórmula.
Passo 5
Essa etapa é só a substituição das três variáveis na lei de Fourier:
Resposta
Exercício Resolvido #4
Michael A. Boles e Yunus A. Çengel, Thermodynamics: An Engineering Approach, 8ª ed. New York: McGraw-Hill Education, 2015, pp. 104-2.92
As temperaturas das superfícies interna e externa de uma janela de vidro x de de espessura no inverno são de e respectivamente. Se a condutividade térmica do vidro for igual a , determine a quantidade de calor perdido, em , através do vidro em um período de .
Passo 1
O exercício pede para determinar a quantidade de calor perdido através do vidro durante um período de . Mas o que isso quer dizer?
A quantidade de calor perdido é como chamam normalmente a quantidade de energia que atravessa o vidro. Essa quantidade é chamada de perdida, porque o fluxo de energia aponta da superfície interna da janela (maior temperatura) para sua superfície externa (menor temperatura). Isso significa que o cômodo protegido pela janela perde essa energia para o ambiente externo. O problema fica melhor explicado pela figura abaixo.
Mas então chegamos em um impasse! A fórmula que conhecemos de transferência de energia por condução (lei de Fourier), só calcula a derivada da energia que é transferida através do vidro em relação ao tempo. Falando de outra forma: essa conta só me dá a quantidade de energia transferida por segundo, não a quantidade transferida em dez horas.
Mas fique calmo que resolveremos esse dificuldade no próximo passo!
Passo 2
Pra resolver esse problema, precisamos perceber que o enunciado não cita nenhuma mudança nas condições de transmissão de energia. Ou seja, essa quantidade permanece constante com o tempo.
Então para fazer a conta, é só achar a energia transferida a cada segundo pela lei de Fourier e multiplicar esse valor pela quantidade de segundos que o período mencionado tem (3600 segundos relativos às 10 horas).
Por essa equação, podemos ver que para encontrar a taxa de calor que atravessa a parede precisamos primeiro achar o valor de três variáveis:
- A condutividade térmica
- A área onde a energia é trocada
- A derivada da temperatura em relação ao eixo
Para fazer isso, a gente precisa obter dois tipos de informação presentes no texto da questão: as informações claras e as que estão escondidos e temos que descobrir por dedução. Esse será nosso próximo passo!
Passo 3
Vamos começar pelas informações mais claras:
- O enunciado diz que a condutividade térmica da janela de vidro vale
- O valor da área também pode ser calculado rapidamente, mas ele não é informado diretamente como o . O tamanho da superfície de troca é mostrado, quando o enunciado expõe as dimensões x do vidro. Ou seja:
- A função das outras três informações ainda não está claramente definida. São elas:
- , a temperatura da superfície interna do vidro
- , a temperatura da superfície externa do vidro
- , a espessura do vidro
As duas primeiras variáveis e , fundamentais para achar , já estão determinadas. Mas como calcular ?
Para essa tarefa, precisamos de dois dados que estão escondidos no enunciado:
- A direção do eixo
- Saber como a temperatura varia nesse eixo
Passo 4
O eixo é a única direção, em que a temperatura do vidro varia. Mas como sabemos que essa simplificação de variação unidirecional da temperatura está sendo usada nesse caso?
Descobrimos isso, quando a questão diz que cada superfície do vidro tem apenas uma temperatura. Uma superfície está a e outra a .
Ou seja, a temperatura de um ponto não varia dentro de uma mesma superfície. Ela só muda, quando a distância entre o ponto considerado e uma das superfície se altera.
Como essa distância só muda conforme caminhamos em uma direção perpendicular às superfícies, o eixo é uma reta perpendicular às superfícies.
Falta agora saber como a temperatura varia ao longo da direção . A única pista do enunciado são as duas temperaturas que ele fornece.
A única função, que pode ser totalmente definida com dois pontos, é uma reta. Por isso, deduzimos que a questão está considerando uma distribuição linear para a temperatura.
No fim, a derivada é igual à inclinação dessa reta!
Passo 5
Agora vamos calcular essa inclinação para determinar . Lembre-se de passar as unidades para o Sistema Internacional de Unidades (SI). Temos então que converter a espessura de centímetro para metro, antes de colocá-la na fórmula.
Passo 6
Essa etapa é só a substituição das três variáveis na lei de Fourier:
Passo 7
Agora é só calcular a quantidade total de energia perdida através de uma regra de três. Se o cômodo perde a cada segundo, quanto de energia ele perde em ?
Antes de dar essa resposta, temos que lembrar de converter esse valor em joule para a unidade pedida: quilojoule.
Resposta
Exercício Resolvido #5
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 96-4.99
Um condensador de grande porte (trocador de calor) de uma central de potência precisa transferir da água que escoa no ciclo de potência para a água bombeada do mar. Admita que a parede de aço que separa a água de circulação da água do mar apresente espessura de , que a condutividade térmica do aço seja igual a e que a diferença máxima de temperatura permitida entre os dois fluidos seja de . Determine a área mínima desse condensador, desprezando a transferência de calor por convecção.
Passo 1
Essa questão é o típico exercício nos informa vários detalhes desnecessários para tentar fazer a gente pensar que ele é mais complicado do que realmente é! O que é uma central de potência? Por que a água que escoa nela vai transferir tanta energia para a água do mar? Não importa! O único fato que realmente faz a diferença é saber que os dois trocam calor separados por uma parede de aço. Isso está ilustrado na figura abaixo.
No fim das contas essa questão só quer saber qual é a área mínima de troca de calor . Podemos chegar nesse valor reorganizando a lei de Fourier.
onde:
Mas como podemos calcular a taxa de variação da temperatura em relação à posição ? Sempre que a questão não informar como a temperatura varia com o eixo , devemos assumir que essa distribuição é linear!
Por causa dessa simplificação, o cálculo de vira:
onde:
Pronto, temos todas as informações para iniciarmos os cálculos. Vamos fazer isso no próximo passo!
Passo 2
Começando as contas pela derivada da temperatura, achamos:
Substituindo esse valor na lei de Fourier reorganizada, encontramos:
Resposta
Exercício Resolvido #6
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 96-4.97
Um aquecedor de água apresenta área superficial igual a e está coberto com uma camada de isolante térmico. As temperaturas interna e externa da camada de isolante são respectivamente iguais a e . Sabendo que o material isolante apresenta condutividade térmica igual a , determine a espessura da camada isolante para que a transferência de calor do aquecedor seja igual a .
Passo 1
O exercício pede para calcular a espessura da camada isolante para que o aquecedor transfira uma determinada taxa de energia por calor à água .
Para isso, devemos recorrer à lei de Fourier e à simplificação que considera a distribuição de temperatura linear.
onde:
- é a espessura do isolante
- é a diferença de temperatura entre as superfícies interna e externa do isolante
- é a condutividade térmica
- é a área superficial onde ocorre a transferência de energia
Substituindo a aproximação da linearidade na fórmula de condução, temos:
Para encontrar a espessura, temos que rearranjar a fórmula deixando a espessura sozinha de um lado e o resto das variáveis do outro.
Depois dessa etapa, veremos com mais facilidade que os quatro dados que devemos obter do enunciado para resolver o exercício são:
No fim, é só substituir os valores dados na fórmula reorganizada de condução para obter o resultado desejado.
Passo 2
Para rearranjar a fórmula simplificada de condução por calor, passamos para o lado esquerdo da equação e para o lado direito.
Passo 3
Essa útima etapa é só a substituição dos dados expostos no enunciado na equação que desenvolvemos.
Atenção! Como os valores substituídos estão de acordo com ao Sistema Internacional de Unidades, o resultado da conta resulta em um valor em metro!
Resposta
Exercício Resolvido #7
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 96-4.96
Uma panela de aço (condutibilidade térmica igual a ) contém água líquida a 15°C. A espessura da panela é uniforme igual a e o diâmetro da panela é 0,2m. A panela é colocada sobre uma resistência elétrica que transfere ao fundo da panela. Admitindo que a temperatura da superfície interna da panela é uniforme e igual , determine a temperatura da superfície inferior externa da panela.
Passo 1
O exercício pede para calcular a temperatura da superfície inferior externa da panela . A função temperatura está presente dentro da derivada na lei de Fourier.
No entanto, recorrendo à simplificação, que considera a distribuição de temperatura como linear, conseguimos calcular a derivada e depois usá-la para calcular a temperatura desconhecida.
onde:
- é a espessura do isolante
- é a temperatura da superfície externa da panela que desejamos calcular
- é a temperatura da superfície interna da panela
- é a condutibilidade térmica
- é a área superficial onde ocorre a transferência de energia
Segue abaixo a ordem das etapas que devemos cumprir para resolver a questão.
- Reorganizar a lei de Fourier, explicitando a derivada da temperatura.
- Substituir nessa fórmula os valores de condutibilidade térmica, da área superficial da base da panela e da taxa de energia fornecida à panela para obter o valor da derivda.
- Reorganizar a relação, que associa a derivada e as temperaturas das superfícies, obtida através da simplificação para explicitar a temperatura da superfície externa.
- Substituir os valores da espessura, da derivada da temperatura e da temperatura da superfície interna da panela pra calcular .
Para cumprir esses passos, é necessário listar o que foi dado pelo enunciado:
- Como o enunciado citou o diâmetro da panela, a forma de sua área, onde ocorre transferência de energia, é circular. Por isso:
Passo 2
Vamos, enfim, rearranjar a lei de Fourier e depois substituir os dados do enunciado para obter a derivada.
Passo 3
Agora a gente tem que reorganizar a expressão de linearização da temperatura e depois substituir as informações coletadas do texto do problema e a derivada da temperatura encontrada no ítem anterior.
Atenção! Antes temos que converter a unidade da espessura de milímetro pra metro.
Resposta
Exercício Resolvido #8
Michael J. Moran, Howard N. Shapiro, Daisie D. Boettner, Margaret B. Bailey, Princípios de Termodinâmica para Engenharia, 7ª ed. Rio de Janeiro: Livros Técnicos e Científicos Editora Ltda., 2013, pp. 62-2.47
Uma parede plana composta consiste em uma camada isolante de de espessura e uma camada de tijolos de de espessura . A temperatura interna relativa ao isolante é . A temperatura externa dos tijolos é . Determine, em regime permanente, a temperatura na interface entre as duas camadas, em °C, e a taxa de transferência de calor através da parede, em por de área de superfície.
Passo 1
A primeira etapa para resolver esse problema é entender o que é uma parede composta. Ela é uma parede com duas camadas. Uma grudada na outra. As superfícies das paredes que estão juntinhas no meio têm a mesma temperatura , porque estão em contato! A primeira informação que o enunciado pede é justamente essa temperatura do meio!
Observe que a figura acima já mostra as temperaturas variando linearmente com o eixo . Essa simplificação foi usada, porque o texto não fala como a temperatura varia! Então, com os dados informados, vamos escrever uma lei de Fourier para cada camada e ver o que temos, o que queremos e o que precisamos encontrar! Para a camada de tijolos, podemos escrever:
onde:
- é a última incógnita do problema
- é a última incógnita do problema
Para a camada de isolante podemos escrever:
onde:
Repare que a variável é a mesma pras duas equações. Por que isso contece se as duas camadas são diferentes? Respoderemos isso no próximo passo.
Passo 2
O enunciado diz que a transferência de calor ocorre em regime permanente! Mas o que isso significa? Significa que a taxa de calor que a camada isolante libera é igual à taxa de calor que a camada de tijolos recebe. Isso quer dizer que:
Ok, mas por que as áreas também são iguais? Por as duas camadas compõe a mesma parede. Ou seja:
Sabendo de tudo isso, conseguimos igualar as duas equações para criar uma fórmula de cálculo da temperatura do meio .
Rearranjando a posição dessas variáveis, achamos:
Com esse valor em mão, usamos a fórmula abaixo para descobrir quanto vale a outra incógnita.
Pronto, agora vamos para o próximo passo para fazer as contas.
Passo 3
Primeiro, vamos calcular quanto vale a temperatura das superfícies internas da parede .
Agora a próxima ingógnita pode ser calculada.