21. Um quilograma de água contida em um conjunto cilindro-pistão passa por dois processos internamente reversíveis em série ilustrados na Fig. P6.21. Para cada processo, determine o trabalho e a quantidade de transferência de calor, amos em kJ.
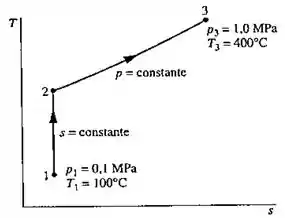
Fig. P6.21
Passo 1
Este é um problema de engenharia em que o a primeira coisa a se pensar é que foi passado de informação no problema para fazer as considerações acerca do processo.
Pelo enunciado, sabe-se que a água está contida no conjunto cilindro-pistão, então não há escoamento, isso quer dizer que o sistema é fechado e não aberto, seria aberto caso houvesse escoamento. Também pelo enunciado, tem-se que os processos são internamente reversíveis. Logo, as considerações sobre o processo que podem ser feitas são:
-Sistema fechado;
-Processos internamente reversíveis;
-Variação de energia cinética e potencial desprezíveis;
Esta última consideração, é uma consideração usual, pois a variação de energia cinética e potencial acaba sendo insignificante frente a variação de energia interna.
Então, como foi dito o sistema é fechado. Assim, para este problema, a equação básica que você vai utilizar para encontrar o trabalho e quantidade de calor transferida vai ser a seguinte:
Onde,
-m é massa do fluido;
-, é a variação de energia interna especifica, em unidades de kJ/kg;
-Q e W são o calor transferido e o trabalho, respectivamente;
Esta equação mostrada é a equação do balanço de energia para sistemas fechados, considerando a variação de energia cinética e potencial desprezíveis.
Passo 2
Então, antes de começar a calcular o trabalho e o calor transferido para cada processo, é preciso saber os processos envolvidos e os estados termodinâmicos.
Se você voltar lá em cima na parte do enunciado, você vai ver a figura P6.21, nela contém os pontos 1, 2 e 3. Estes pontos representam os estados termodinâmico do sistema, e o que seria este estado termodinâmico? Estado termodinâmico significa as condições de temperatura e pressão em um determinado ponto do processo global, que será usado para definir as propriedades termodinâmicas, como entalpia, entropia e energia interna, por exemplo.
Estes pontos delimitam o início e o final do processo, assim do ponto 1 ao ponto 2 temos um processo e do ponto 2 ao ponto 3 temos outro processo. Logo, temos o processo 1-2, na qual tem que encontrar o trabalho W12 e o calor Q12, e o processo 2-3, que você deve encontrar o trabalho W23 e o calor Q23.
Passo 3
Entender como cada processo ocorre pode te ajudar a saber como determinar o trabalho e o calor em cada processo.
Assim, a seguir é feita uma descrição de cada processo conforme o gráfico da fig. P6.21 para você estabelecer a estratégia de cálculo para o trabalho e o calor.
-Processo 1-2:
É um processo isentrópico, pois a entropia é constante ao longo dele, isso você pode ver pelo gráfico da fig. P6.21, lá em cima, que a entropia, colocada no eixo x, não se altera do ponto 1 ao 2, isto é, no ponto 1 e no ponto 2 o valor da entropia é o mesmo.
Como se trata de um processo isentrópico, então você pode usar a relação matemática entre variação de entropia e calor, aplicada a sistemas fechados e processos internamente reversíveis, que é caso, segundo o enunciado. A relação matemática entre variação de entropia e calor para sistemas fechados e processos internamente reversíveis é:
Como a entropia não varia do estado 1 ao estado 2, então a integral é nula, sendo assim já é possível encontrar o valor para Q12, que é zero.
Agora que você sabe que o Q12 é zero, você pode pegar aquela equação do balanço de energia pera sistemas fechados e determinar o trabalho.
Onde,
- e , são a energia interna especifica do estado 2 e do estado 1, respectivamente, que você vai achar através de tabelas de dados termodinâmicos, que será mostrado no passo 4.
-Processo 2-3:
É um processo isobárico, sendo que isobárico significa pressão constante, como definido na figura P6.21. Então, a pressão no estado 2 e no estado 3 são iguais, p2=p3.
Como o processo 2-3 é a pressão constante, então você pode usar a equação do trabalho em função da pressão e do volume que é:
Resolvendo a integral com a pressão sendo constante, a expressão para o trabalho W23 ficando da forma:
Onde,
-v3 e v2, são o volume especifico do estado 3 e do estado 2, respectivamente, e da mesma forma como a energia interna, você vai achar seus valores a partir de uma tabela de dados termodinâmicos.
Com o trabalho W23 definido você pode usar o balanço de energia para sistemas fechados e achar o calor Q23.
Portanto, tem-se todas as expressões para determinar o trabalho e o calor transferido em cada processo, basta agora encontrar os dados termodinâmicos nas tabelas, definindo os estados termodinâmicos.
Passo 4
Agora é definir os estados termodinâmicos.
Antes de definir, vale lembrar que para determinar um valor de uma variável termodinâmica em um certo estado, você precisa de conhecer no mínimo dois valores de outras variáveis termodinâmica nesse mesmo estado.
-Estado 1
Para o estado 1 já temos a temperatura e a pressão, dados no enunciado
Será preciso encontrar a energia interna especifica e a entropia do estado 1. Para isso, você vai encontrar na tabela o valor de U1 e de S1 correspondentes aos valores de T1 e p1.
Pela Tabela A-4 do livro Shapiro-Princípios da Termodinâmica, 7ª Edição:
-Estado 2
Do estado 2, você vai precisar da energia interna especifica e do volume especifico. Desse estado, sabe-se que a entropia é igual ao do estado 1 e também que a pressão do estado 2 é igual a pressão do estado 3, e como temos o valor da entropia do estado 1 e pressão do estado 3 (dado no enunciado), logo temos os valores de entropia e a pressão do estado 2.
Assim, com esses valores você consegue achar a energia interna e o volume especifico desse estado.
Pela Tabela A-4 do livro Shapiro-Princípios da Termodinâmica, 7ª Edição:
-Estado 3
Para este estado precisa da energia interna especifica e do volume especifico.
Como dado no enunciado, a temperatura e a pressão do estado 3 são
Pela Tabela A-4 do livro Shapiro-Princípios da Termodinâmica, 7ª Edição:
Agora com todos os estados definidos e as expressões estabelecidas, é só calcular.
Passo 5
-Processo 2-1:
Como mostrado lá no passo 3:
Aplicando os valores
-Processo 2-3
Sendo
Aplicando os valores
Aplicando os valores