23. Uma libra-massa (0,45 kg) de água em um conjunto cilindro-pistão inicialmente como líquido saturado a 1 atm passa por uma expansão internamente reversível a pressão constante até x = 90%. Determine o trabalho e o calor transferido, ambos em Btu. Esboce o ciclo em coordenadas p-v e T-s. Relacione o trabalho e a quantidade de calor transferida a áreas nesses diagramas.
Passo 1
Como primeiro passo na resolução deste problema, você deve analisar o que foi dito no enunciado para ver o que de informações foi passada para que você possa fazer as considerações e assim começar a resolver a questão.
Do enunciado sabe-se que a água está em no conjunto cilindro-pistão, dessa forma o sistema desse processo é um sistema fechado, pois em um sistema cilindro-pistão o fluido fica contido no cilindro sem haver fluxo para dentro e nem para fora.
O enunciado também diz que é um processo de expansão internamente reversível a pressão constante, e além disso que a água no início se encontra como líquido saturado e no final do processo se encontra com um título de 90%. Lembrando que o título significa a quantidade percentual de vapor em uma mistura binária líquida-vapor, ou seja, no estado final a água se encontra como uma mistura de líquido e vapor, contendo 90% de vapor e 10% de líquido.
As considerações que você pode assumir para processo, então podem ser as seguintes:
-Sistema fechado;
-Processo internamente reversível;
-Expansão a pressão constante;
-Variação de energia cinética e potencial desprezíveis.
Passo 2
O passo seguinte é estabelecer a estratégia de cálculo com base nas considerações feitas.
Para encontrar o trabalho e o calor transferido, você pode pegar a equação do balanço de energia para sistemas fechados, já que o processo em questão se trata de um sistema fechado. A equação do balanço de energia para sistemas fechado é:
Onde,
-m é massa do fluido;
-, é a variação de energia interna especifica, em unidades de kJ/kg;
-Q e W são o calor transferido e o trabalho, respectivamente;
Abrindo a equação anterior vai ficar assim:
Assim, você precisará dos valores de energia interna especifica nos estados 1 e 2, isso você pode encontrar a partir de tabelas de dados termodinâmicos, bastando os estados termodinâmicos estarem definidos.
Você também vai precisar do valor do trabalho ou do valor do calor transferido para conseguir calcular ou o trabalho, ou o calor transferido. Então, como pode ver, vai precisar de outra equação. Uma que você pode usar é aquela que relaciona o trabalho com a pressão e com o volume, que é a seguinte:
Resolvendo a integral, levando em conta que a pressão é constante, então a integral resolvida fica da forma a seguir:
Onde,
-v2 é o volume especifico do estado 2;
-v1 é o volume especifico do estado 1;
Da mesma forma que para a energia interna especifica, os volumes específicos podem ser determinados por tabelas de dados termodinâmicos.
Portanto, você tem as expressões para o cálculo, falta agora determinar os estados para encontrar os valores necessários nas tabelas.
Passo 3
Bem, agora é estabelecer os estados termodinâmicos. Estes estados termodinâmicos nada mais são do que as condições de pressão e temperatura de um certo ponto do processo. No caso, são apenas dois estados, o estado inicial (estado 1) e o estado final (estado 2).
-Estado 1
Neste estado a água se encontra como líquido saturado, isso quer dizer que é necessário apenas um valor de uma propriedade termodinâmica para encontrar qualquer outro valor. No enunciado foi dito que a pressão nesse estado é de 1 atm. Lembrando que 1 atm é equivalente a 1,014 bar e a 101,325 kPa. Assim, com algum desse valor, conforme a unidade, você consegue encontrar em tabelas de água saturada os valores necessários para o cálculo, que são para energia interna especifica e volume especifico.
Pela Tabela A-2 do livro Shapiro-Princípios da Termodinâmica, 7ª Edição:
-Estado 2
O estado 2 é um estado em que a água se encontra como uma mistura de líquido e vapor, com um título de 90%, isto é, com 90% de vapor na mistura. Para esse caso, a determinação das propriedades termodinâmicas dependerá de dois outros valores de outras propriedades termodinâmicas. Sabemos que a pressão nesse estado é mesma do estado 1, que é 1,0 atm. E também sabemos que o título é de 90%. Logo, já temos os dois valores necessários.
Para encontrar o volume especifico e a energia interna especifica no estado 2, você terá que usar a definição matemática de título para encontrar o que precisa, que é
Explicitando o termo de v2:
Analogamente,
Onde,
-x é o título;
-vl é o volume especifico do líquido saturado;
-vg é o volume especifico do vapor saturado;
-, é a energia interna especifica do líquido saturado;
-, é a energia interna especifica do vapor saturado;
Os valores de volume especifico e energia interna especifica para o líquido saturado e vapor saturado, é encontrado diretamente nas tabelas de água saturada na pressão de 1,0 atm=1,0 bar=101,325 kPa.
Pela Tabela A-2 do livro Shapiro-Princípios da Termodinâmica, 7ª Edição:
Calculando v2:
Calculando :
Passo 4
Agora é só aplicar os valores nas equações.
-Trabalho
Aplicando os valores
-Calor Transferido
Aplicando os valores
Passo 5
Foi pedido no enunciado a unidade final em Btu, logo é necessária uma conversão de kJ para Btu.
Como fator de conversão, pode-se usar que 1,0 kJ equivale a 0,9478 Btu, assim
Passo 6
Plotando os gráficos p-v e T-s:
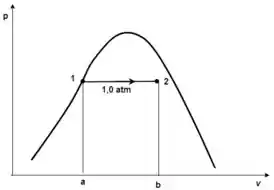
O trabalho é representado geometricamente pela área a-b-2-1-a do diagrama p-v e o calor transferido é representado geometricamente pela área 1-c-d-2-1 do diagrama T-s.