32. Ar em um conjunto cilindro-pistão é submetido a um ciclo de potência de Carnot. Os processos isotérmicos de expansão e compressão ocorrem a 1400K e 350K, respectivamente. As pressões no início e no final da compressão isotérmica são 100 kPa e 500 kPa, respectivamente. Admitindo o modelo de gás ideal, com cp=1,005 kJ/kg.K, determine
A) A pressão no início e no final da expansão isotérmica, ambas em kPa.
B) A quantidade de calor transferida e o trabalho, em kJ/kg, para cada processo.
C) A eficiência térmica.
Passo 1

Antes de iniciarmos os cálculos, vamos relembrar como é o ciclo de Carnot.
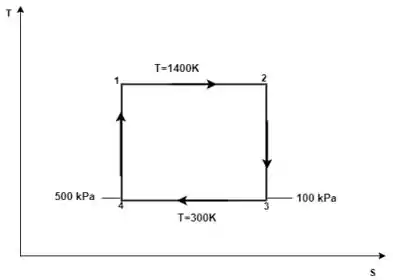
Um ciclo de potência de Carnot é dado pelos processos 1-2, 2-3, 3-4 e 4-1 do diagrama T-S, descritos como:
-Processo 1-2: Expansão isotérmica;
-Processo 2-3: Resfriamento isentrópico (entropia constante);
-Processo 3-4: Compressão isotérmica;
-Processo 4-1: Aquecimento isentrópico (entropia constante);
Passo 2
Para a resolução do problema, é válido estabelecer as considerações acerca do processo.
As considerações que podem ser feitas são:
-cp constante;
-Sistema fechado, pois o gás se encontra em um conjunto cilindro-pistão;
-Modelo de gás ideal para o ar;
-Variações de energia cinética e potencial desprezíveis;
Passo 3
A)
Do enunciado, foi pedido a pressão inicial e final do processo de expansão isotérmica (Processo 1-2), então o que você precisa achar nessa questão são as pressões p1 e p2.
Pelo diagrama, temos que o processo 4-1 (aquecimento isentrópico) e 2-3 (resfriamento isentrópico) ocorrem sem variação de entropia, isso é intrínseco do ciclo de potência de Carnot. Assim,
Vamos lembrar que a variação de entropia de um estado a outro, se relaciona com as temperaturas e pressões dos respectivos estados pela seguinte expressão
Onde,
-, é a variação de entropia especifica do estado 1 ao estado 2;
-cp é o calor especifico a pressão constante;
-T1 e T2 são a temperatura do estado 1 e estado 2, respectivamente;
-p1 e p2 são a pressão do estado 1 e estado 2, respectivamente;
-R é a constante dos gases ideais dividido pela massa molar do gás;
Essas equações são usadas somente para modelo de gás ideal e calores específicos constantes.
Para você não precisar calcular a variação de entropia, para determinar as pressões, você pode aplicar a equação acima aos estados 1 e 4, e depois aplicar aos estados 2 e 3, que assim as varrições de entropia serão nulas, pois S1=S4 e S2=S3.
Passo 4
Vamos agora aplicar a equação da variação de entropia aos estados mencionados, para encontrar expressões explicitas para p1 e p2
-Processo 4-1:
Aplicando exponencial em ambos os lados
Lembrando que exponencial de logaritmo (ln), a função exponencial e ln, se anulam, pois uma é inversa da outra, e o que sobre é a função dentro de ln, assim
Isolando p1
-Processo 2-3:
Analogamente, você vai chegar na expressão para p2
Passo 5
Antes de aplicar os valores vamos pegar os dados fornecidos.
Sendo que R é a constante dos gases ideais dividido pela massa molar do gás (ar). A constante dos gases ideais você pode usar o valor de 8,314 kJ/kmol K, e a massa molar do ar é 29,0 kg/kmol
Aplicando os valores:
Passo 6
B)
-Processo 1-2: Expansão isotérmica (T1=T2)
Quando fala que um processo se trata de expansão ou compressão isotérmica (T constante), para o cálculo do calor transferido você pode usar a relação matemática entre calor e variação de entropia, que é a seguinte
Você resolvendo esta integral para T constante, então a expressão fica assim
Onde, T= T1=T2=1400 K.
Voltando a questão (A), você usou uma expressão da variação de entropia em função das pressões e temperaturas, você vai usa-la aqui novamente
Substituindo,
Como T1=T2, então o termo da ln se anula, pois ln(1) é zero
Para você encontrar o trabalho, basta você usar o balanço de energia para sistemas fechados.
Onde,
-m é massa do fluido;
-, é a variação de energia interna especifica, em unidades de kJ/kg;
-, é a variação de energia cinética especifica, em unidades de kJ/kg;
-, é a variação de energia potencial especifica, em unidades de kJ/kg;
Pelas considerações de que as variações de energia cinética e potencial são desprezíveis, pois suas variações são insignificantes perante a variação de energia interna, então estes termos se anulam, ficando o balanço de energia como
Como o gás foi considerado um gás ideal, então a variação de energia interna depende apenas da variação de temperatura, e como
Então,
Assim,
Passo 7
-Processo 2-3: Resfriamento Isentrópico (S2=S3)
Pela relação já mostrada
Assim, o calor se anula, pois não a variação de entropia especifica
Para o trabalho, basta você usar a equação do balanço de energia
Como Q23=0
A energia interna para um gás ideal depende somente da temperatura, então você pode usar a seguinte expressão para a variação de energia interna em função da variação da temperatura
Onde,
-cV é o calor especifico;
O calor especifico pode ser determinado pela seguinte expressão
Então, para o trabalho no processo 2-3:
Aplicando os valores
Passo 8
-Processo 3-4: Compressão isotérmica (T3=T4)
Analogamente, ao que foi feito no Processo 1-2.
Você resolvendo esta integral para T constante, então a expressão fica assim
Onde, T= T4=T3=350 K.
Substituindo,
Como T3=T4, então o termo da ln se anula, pois ln(1) é zero, então
Para o trabalho:
Então,
Assim,
Passo 9
-Processo 4-1: Aquecimento Isentrópico (S4=S1)
Analogamente, ao que foi feito no processo 2-3
Assim, o calor se anula, pois não a variação de entropia especifica
Para o trabalho,
Onde,
-cV é o calor especifico;
O calor especifico pode ser determinado pela seguinte expressão
Então, para o trabalho no processo 4-1:
Aplicando os valores
Passo 10
C)
Calculando e eficiência térmica:
A eficiência térmica, ηT, em um processo de ciclo de potência representa o quanto de energia disponível foi usado para gerar trabalho útil. Uma expressão para sua obtenção é função das temperaturas fria (menor) e quente (maior), o que foi dado, assim
Substituindo os valores,
Resposta
A)
B)
-Processo 1-2
-Processo 2-3
-Processo 3-4
-Processo 4-1
C)