Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 2.Problemas - Ex. 54
Uma escada rolante de um centro comercial foi projetada para transportar 30 pessoas com 75 kg cada, à velocidade constante de 0,8 m/s e inclinação de 45°. Determine a potência mínima necessária para mover essa escada rolante. Qual seria a resposta caso a velocidade da escada precisasse ser duplicada?
Passo 1
Temos que a expressão para o balanço de energia é dada por:
Como pode sempre haver um número diferente de pessoas na escada, o sistema não está em regime permanente. Veja que na saída não irá existir nenhuma transferência de energia na saída, as pessoas apenas vão sair, existe apenas a transferência de energia na entrada, que é a energia necessária para movimentar a escada. Então, nosso balanço fica da seguinte forma
Passo 2
Note que, para fazer a escada rolante funcionar, ela precisa de uma certa potência mínima, lembrando que potência é dada por
No nosso balanço, a energia necessária para fazer a escada funcionar é a potência da energia potencial, pois haverá uma diferença na altura do sistema. Assim
Temos que a razão entre nos fornece a velocidade vertical do sistema, ou seja, a componente vertical da velocidade. Assim, a nossa expressão ficará da seguinte forma
Passo 3
Para descobrirmos a velocidade vertical, vamos utilizar o seguinte esquema
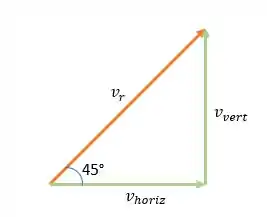
Note que, a velocidade vertical está oposta ao ângulo de 45°, assim
Passo 4
Considerando a carga máxima que a escada pode carregar, temos:
Agora, substituindo na nossa expressão, teremos:
Temos que 1 kJ/s equivale a 1 kW, assim:
Passo 5
Se duplicássemos a velocidade da escada, teríamos que a velocidade vertical seria:
Assim, a potência seria:
A potência também dobra, aproximadamente.
Resposta
A potência mínima para a escada funcionar é de 12,48 kW, caso dobrássemos a velocidade de operação da escada, a potência praticamente também dobraria, sendo utilizado 24,92 kW.