Limites Laterais e Existência do Limite
Produzido por Philip Canabarro BlockerTeoria
Limites Laterais
Imagine:
Veja o que acontece com a função próximo do ponto :
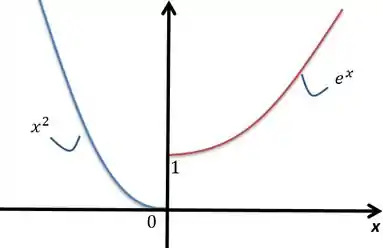
Se você tentar aproximar o a zero, vamos ter um probleminha. Você pode ver que a função tem tendências diferentes naquele ponto. Pela esquerda, é o . Pela direita, . Daí surge uma pergunta: queremos aproximar por onde? Pela esquerda ou pela direita?
Aí surge a notação dos limites laterais. Se aproximarmos para um número por valores maiores que , ou seja, pela direita, estamos tendendo a. Aí usamos a notação com o “”.
Da mesma forma, se aproximarmos de um número por valores menores que , ou seja, pela esquerda, estamos tendendo a. A usamos a notação com “”.
Voltando ao desenho do gráfico, você vai perceber que a tendência do limite quando observarmos pela direita é ir para . Essa tendência pela esquerda será a de ir para .
Agora vai para os exercícios praticar!
Existência do Limite
No exemplo anterior, vimos que os limites laterais não batem!
Bom, mas se os limites laterais são diferentes, como no exemplo anterior, o que acontece com o limite mesmo, em questão?
Nesse caso, o limite não existe! Mas, por que?
Existem duas regras que o limite deve seguir para existir:
Limites laterais não podem explodir para .
Limites laterais devem possuir o mesmo valor.
Apenas quando os limites seguem essas duas condições, podemos afirmar que existem.
No exemplo inicial, os limites laterais não explodem para , respeitando a primeira condição. Porém, eles não convergem para o mesmo valor:
Logo o limite não vai existir! De maneira geral, um limite existe se:
EXERCÍCIOS, EXERCÍCIOS, EXERCÍCIOS!
Existência do Limite
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Determine a porcentagem de ar teórico necessária para queimar de em uma combustão completa que gera de oxigênio nos produtos.
Passo 1
Oi, lind@s! Vamos fazer um exercício de cálculo de porcentagem de ar teórico?
Para calcular a porcentagem de ar teórico, temos que dividir a quantidade de de ar que está presente na combustão pela quantidade de de ar teórico.
A quantidade de ar teórico é a quantidade de ar necessária pra fazer do combustível passar por uma combustão completa sem gerar nos produtos. Ou seja, é encontrada balanceando a equação de combustão abaixo.
onde , , e são os coeficientes estequiométricos da equação química da combustão.
Como o ar é composto de e , a quantidade de de ar é a soma entre a quantidade de de do ar e a quantidade de de .
Pra achar a quantidade de ar seco da combustão do enunciado, balanceamos a equação de combustão que gera de nos produtos.
onde , , e são os coeficientes estequiométricos da equação da combustão do enunciado.
Nesse caso, é encontrado a partir de uma fórmula parecida com a equação de .
Vamos iniciar as contas, fazendo o balanceamento dessa última equação de combustão pra achar .
Passo 2
Fazer o balanço da equação é a mesma coisa que fazer os elementos químicos do lado esquerdo terem a mesma quantidade de que dos elementos químicos do lado direito! Ou seja, a quantidade de do lado esquerdo deve ser igual à quantidade de do lado direito. Por isso, de dos reagentes deve ser igual a de dos produtos.
A quantidade de de é encontrada através do balanço de hidrogênio . Para a quantidade de ficar balanceada, os de dos reagentes devem ser iguais aos de dos produtos.
O coeficiente pode ser encontrado fazendo o balanço de oxigênio . Pra isso, os de presentes nos reagentes têm que ser iguais aos de dos produtos.
Substituindo na fórmula de :
Agora podemos achar no próximo passo e calcular a porcentagem de ar teórico usada na combustão!
Passo 3
Começamos as nossas contas pra achar , calculando através do balanço de carbono .
Para a quantidade de ficar balanceada, de dos reagentes deve ser igual a de dos produtos.
Antes de achar o coeficiente , precisamos calcular o coeficiente através do balanço de hidrogênio ! De acordo com esse balanço, os de dos reagentes precisam ser iguais aos de dos produtos.
O coeficiente pode ser encontrado fazendo o balanço de oxigênio . Pra isso, os de presentes nos reagentes têm que ser iguais aos de dos produtos.
Substituindo na fórmula de :
Por fim, substituindo e na equação da porcentagem de ar teórico:
Resposta
Exercício Resolvido #2
Elaboração própria
de gás metano sofre uma combustão completa com de excesso de ar. Determine a equação balanceada dessa combustão.
Passo 1
Fala, galera! Vamos aprender a usar porcentagem de ar teórico através de um exercício?

O primeiro passo de qualquer exercício de combustão é escrever a equação da reação. Pra isso, devemos conhecer os reagentes e produtos. No nosso caso, a questão disse que e ar seco reagem na combustão. Logo, , do ar e do ar são os reagentes. Como a combustão é completa, os produtos são , , e ( é por causa do excesso de ar).
, , , e são os coeficientes estequiométricos da combustão. Fazer o balanceamento da equação é a mesma coisa que achar o valor desses coeficientes.

No entanto, para calcular todos esses coeficientes, precisamos descobrir quanto vale a quantidade de ar teórico. é a quantidade de ar necessária pra fazer os de passar por uma combustão completa sem gerar nos produtos. Ou seja, é encontrada balanceando a equação de combustão abaixo.
onde , , e são os coeficientes estequiométricos da equação da combustão do enunciado.
Como o ar é formado por e , pode ser obtido, somando a quantidade de de com a quantidade de de .
Vamos começar o exercício, calculando no próximo passo através do balanceamento dessa última equação de combustão!
Passo 2
Fazer o balanço da equação é a mesma coisa que fazer os elementos químicos do lado esquerdo terem a mesma quantidade de que dos elementos químicos do lado direito! Ou seja, a quantidade de do lado esquerdo deve ser igual à quantidade de do lado direito. Por isso, de dos reagentes deve ser igual a de dos produtos.
A quantidade de de é encontrada através do balanço de hidrogênio . Para a quantidade de ficar balanceada, os de dos reagentes devem ser iguais aos de dos produtos.
O coeficiente pode ser encontrado fazendo o balanço de oxigênio . Pra isso, os de presentes nos reagentes têm que ser iguais aos de dos produtos.
Substituindo na fórmula de :
Beleza, achamos o ar teórico ! Mas como isso pode nos ajudar a balancear a primeira equação do passo 1? Veremos isso no próximo passo!
Passo 3
A gente vai usar pra encontrar o coeficiente ! Pra isso, nós temos que usar um dado muito importante que o enunciado nos deu! Ele disse que a combustão foi feita com de excesso de ar. Isso significa que foram usados de ar teórico na queima de ! Com essa informação, somos capazes de achar a quantidade de ar usado na combustão.
Agora que vem o pulo do gato! Vamos usar a fórmula de pra achar o coeficiente !
Aeeee! Achamos o coeficiente da equação que queremos balancear! Agora nos resta calcular os outros coeficientes no próximo passo!
Passo 4
Para a quantidade de ficar balanceada, de dos reagentes deve ser igual a de dos produtos. A equação da combustão se encontra abaixo pro balanceamento ficar mais claro.
Antes de achar o coeficiente , precisamos calcular o coeficiente através do balanço de hidrogênio ! De acordo com esse balanço, os de dos reagentes precisam ser iguais aos de dos produtos.
O coeficiente pode ser encontrado fazendo o balanço de oxigênio . Pra isso, os de presentes nos reagentes têm que ser iguais aos de dos produtos.
Por fim, achamos o coeficiente do dos produtos, igualando os de dos reagentes com os de dos produtos.
Substituindo os coeficientes na equação de combustão, encontramos a equação balanceada que o enunciado nos pediu!
Resposta
Exercício Resolvido #3
Elaboração própria
Em uma combustão, n-octano é queimado com de excesso de ar. Determine a equação balanceada dessa combustão.
Passo 1
Oi, querid@s! Bora aprender a usar porcentagem de ar teórico através de um exercício?

O primeiro passo de qualquer exercício de combustão é escrever a equação da reação. Pra isso, devemos conhecer os reagentes e produtos. No nosso caso, a questão disse que e ar seco reagem na combustão. Logo, , do ar e do ar são os reagentes. Os produtos são , , e , porque supomos a combustão completa. Veja a equação dela abaixo.
, , , e são os coeficientes estequiométricos da combustão do enunciado. Fazer o balanceamento da equação é a mesma coisa que achar o valor desses coeficientes.

No entanto, para calcular todos esses coeficientes, precisamos descobrir quanto vale a quantidade de ar teórico. é a quantidade de ar necessária pra fazer de passar por uma combustão completa sem gerar nos produtos. Ou seja, é encontrada balanceando a equação de combustão abaixo.
onde , , e são os coeficientes estequiométricos da equação da combustão sem excesso de ar.
Como o ar é formado por e , pode ser obtido, somando a quantidade de de com a quantidade de de .
Vamos começar o exercício, calculando no próximo passo através do balanceamento dessa última equação de combustão!
Passo 2
Fazer o balanço da equação é a mesma coisa que fazer os elementos químicos do lado esquerdo terem a mesma quantidade de que dos elementos químicos do lado direito! Ou seja, a quantidade de do lado esquerdo deve ser igual à quantidade de do lado direito. Por isso, de dos reagentes deve ser igual a de dos produtos.
A quantidade de de é encontrada através do balanço de hidrogênio . Para a quantidade de ficar balanceada, os de dos reagentes devem ser iguais aos de dos produtos.
O coeficiente pode ser encontrado fazendo o balanço de oxigênio . Pra isso, os de presentes nos reagentes têm que ser iguais aos de dos produtos.
Substituindo na fórmula de :
Beleza, achamos o ar teórico ! Mas como isso pode nos ajudar a balancear a primeira equação do passo 1? Veremos isso no próximo passo!
Passo 3
A gente vai usar pra encontrar o coeficiente ! Pra isso, nós temos que usar um dado muito importante que o enunciado nos deu! Ele disse que a combustão foi feita com de excesso de ar. Isso significa que foram usados de ar teórico na queima de ! Com essa informação, somos capazes de achar a quantidade de ar usado na combustão.
Agora que vem o pulo do gato! Vamos usar a fórmula de pra achar o coeficiente !
Aeeee! Achamos o coeficiente da equação que queremos balancear! Agora nos resta calcular os outros coeficientes no próximo passo!
Passo 4
Para a quantidade de ficar balanceada, de dos reagentes deve ser igual a de dos produtos. A equação da combustão se encontra abaixo pro balanceamento ficar mais claro.
Antes de achar o coeficiente , precisamos calcular o coeficiente através do balanço de hidrogênio ! De acordo com esse balanço, os de dos reagentes precisam ser iguais aos de dos produtos.
O coeficiente pode ser encontrado fazendo o balanço de oxigênio . Pra isso, os de presentes nos reagentes têm que ser iguais aos de dos produtos.
Por fim, achamos o coeficiente do dos produtos, igualando os de dos reagentes com os de dos produtos.
Substituindo os coeficientes na equação de combustão, encontramos a equação balanceada que o enunciado nos pediu!
Resposta
Exercício Resolvido #4
Michael A. Boles e Yunus A. Çengel, Termodinâmica, 7ª ed. Porto Alegre: AMGH EDITORA LTDA., 2013, pp. 802-15-33(b)
Carbono é queimado com ar seco. A análise volumétrica dos produtos é de de , de , de e de . Determine (b) a porcentagem de ar teórico utilizado.
Passo 1
E aííí, fof@s! Indo direto ao ponto, o exercício quer que a gente calcule a quantidade de de ar usado na combustão dividida pela quantidade de de ar teórico. Essa divisão é chamada de porcentagem de ar teórico e é calculada pela fórmula abaixo.
é encontrada a partir da equação da combustão que o enunciado cita. O enunciado diz que o carbono reage com o e o do ar seco pra formar os seguintes produtos: , , e . A equação de reação abaixo mostra os reagentes e produtos dessa combustão.
onde , , , , e são os coeficientes estequiométricos da reação.
Como o ar seco é formado por e , achamos a quantidade de de ar, somando a quantidade de de com a quantidade de de .
é a quantidade de ar necessária pra fazer o carbono passar por uma combustão completa sem gerar nos produtos. Ou seja, é encontrada balanceando a equação de combustão abaixo.
onde , e são os coeficientes estequiométricos da equação da combustão do enunciado.
Como o ar é formado por e , pode ser obtido, somando a quantidade de de com a quantidade de de .
Vamos começar o exercício, balanceando a primeira equação de combustão e encontrando !
Passo 2
O primeiro passo para balancear uma equação de combustão com a composição dos produtos conhecida é achar a quantidade de de cada componente dos produtos. Pra isso, supomos que de produto é gerado na combustão. Assim, achamos a quantidade de de multiplicando os de produto pelos de .
Também somos capazes de achar a quantidade de de , multiplicando os de produto pelos de presente nos produtos secos.
Por fim, achamos os coeficientes do e do , multiplicando os de produto pelas porcentagens desses gases nos produtos.
Pra quantidade de ficar balanceada, os de dos reagentes têm que ser iguais aos de dos produtos. Observe a equação de combustão abaixo para visualizar melhor o balanceamento.
O coeficiente é encontrado através do balanço de oxigênio . Os de dos reagentes têm que ser iguais aos de dos produtos.
Agora sim somos capazes de achar a quantidade de ar teórico que queima os de completamente!
Acharemos no próximo passo através do balanceamento dessa última equação de combustão!
Passo 3
Pra quantidade de carbono ficar balanceada, a quantidade de do lado esquerdo deve ser igual à quantidade de do lado direito.
Por isso, de dos reagentes deve ser igual a de dos produtos.
O coeficiente pode ser encontrado fazendo o balanço de oxigênio . Pra isso, os de presentes nos reagentes têm que ser iguais aos de dos produtos.
Substituindo na fórmula de :
Substituindo e na equação de porcentagem de ar teórico:
Beleza, achamos a porcentagem de ar teórico! Estamos de parabéns!
Resposta
Exercício Resolvido #5
Michael A. Boles e Yunus A. Çengel, Termodinâmica, 7ª ed. Porto Alegre: AMGH EDITORA LTDA., 2013, pp. 802-15-28
Uma mistura de combustível de em massa de metano e em massa de etanol é totalmente queimada com ar teórico. Considerando que o fluxo total do combustível é de , determine o fluxo de ar necessário.
Passo 1
Fala, man@! Tudo belezinha? Sem enrolação, vamos tentar entender logo a questão!

O primeiro passo de qualquer exercício de combustão é escrever a equação da reação. O enunciado diz que o combustível passa por uma combustão completa com ar teórico. Isso quer dizer que a reação é feita sem excesso de ar. Logo, apenas , e são os produtos. Como o ar é feito de e , os reagentes são , , e . A equação da reação é:
onde , , , , e são os coeficientes estequiométricos da combustão.
O enunciado quer que a gente calcule o fluxo de ar (massa de ar que é usada na combustão a cada segundo), mas para achar , precisamos achar a quantidade de de ar que é usada a cada segundo . é encontrada, através da fórmula abaixo.
Pra gente converter pro fluxo , basta multiplicar pela massa molar do ar. Essa massa molar pode ser encontrada em tabelas de gases ideais de livros. Ela vale . Agora que sabemos tudo isso, vamos começar a calcular , balanceando a equação de combustão!
Passo 2
O primeiro passo para fazer o balanço de uma equação, quando o enunciado nos dá as composições dos produtos e do combustível, é determinar os coeficientes de cada componente do combustível. Os coeficientes são encontrados, calculando os fluxos de cada componente.

Calcularemos , achando o fluxo de presente no combustível. Encontramos multiplicando os de combustível pelos de no combustível.
Da mesma forma, achamos o fluxo de , multiplicando pelos de no combustível.
Agora, para achar a quantidade de de nos reagentes, dividimos pela massa molar do metano que vale segundo tabelas de gases ideais de livros.
é encontrado, dividindo pela massa molar do etanol que vale segundo as tabelas termodinâmicas de gases.
Substituindo o valor desses coeficientes calculados na equação de combustão:
Com esses coeficientes já somos capazes de achar os coeficientes restantes!
Passo 3
Achamos o coeficiente , fazendo o balanço do carbono . Para a quantidade de carbono ficar balanceada, os de dos reagentes deve ser igual a de dos produtos.
A quantidade de de é encontrada através do balanço de hidrogênio . Para a quantidade de ficar balanceada, os de dos reagentes devem ser iguais aos de dos produtos.
O coeficiente pode ser encontrado fazendo o balanço de oxigênio . Pra isso, os de presentes nos reagentes têm que ser iguais aos de dos produtos.
Substituindo na fórmula de :
Multiplicando por , achamos o fluxo de ar que o enunciado pediu!
Boooooooa, garot@! Achamos a resposta!!
Resposta
Exercício Resolvido #6
Michael A. Boles e Yunus A. Çengel, Termodinâmica, 7ª ed. Porto Alegre: AMGH EDITORA LTDA., 2013, pp. 802-15-31(b)
Um combustível gasoso com análise volumétrica de de , de e de é queimado completamente com de ar teórico. Determine (b) a fração de vapor de água que condensaria caso os gases do produto fossem resfriados a e .
Passo 1
Fala, gente! Vamos começar sem enrolação! O primeiro passo de qualquer exercício de combustão é entender quais são os reagentes e os produtos. O enunciado diz que , e reagem com o ar que é formado por e . Logo, , , e são os reagentes. Como é dito que a combustão é completa com excesso de ar, , , e são produtos.
onde , , , , , , , são os coeficientes estequiométricos da reação.
Pra achar a fração de vapor de água condensada , temos que encontrar a quantidade total de de no produto. A fração é igual a quantidade de água condensada dividida pela quantidade total de de água.
No próximo passo, vamos começar nosso caminho pra encontrar .
Passo 2
O primeiro passo para fazer o balanço de uma equação com combustível misturado é determinar a quantidade de dos componentes que formam o combustível. Ou seja, temos que achar de de , a quantidade de de e a quantidade de de presentes dentro da mistura combustível. Ouçam bem essa dica que estou dando!

Achamos a quantidade de de , supondo que de combustível é queimado. A quantidade real de combustível queimado não vai interferir no cálculo de , então podemos assumir o valor que quisermos. Calculamos , multiplicando os de combustível pelos de no combustível.
Da mesma forma, achamos a quantidade de de , multiplicando os pelos de no combustível. A quantidade de de é encontrada, multiplicando os pelos de no combustível!
Substituindo essas informações na equação química de combustão, encontramos a seguinte reação.
Agora, vamos aprender a encontrar o coeficiente nos próximos passos, usando a porcentagem de ar teórico que o enunciado informa!
Passo 3
Para calcular , precisamos descobrir quanto vale a quantidade de ar teórico. é a quantidade de ar necessária pra fazer de combustível passar por uma combustão completa sem gerar nos produtos. Ou seja, é encontrada balanceando a equação de combustão abaixo.
onde , , e são os coeficientes estequiométricos da equação da combustão sem excesso de ar.
Como o ar é formado por e , pode ser obtido, somando a quantidade de de com a quantidade de de .
Vamos calcular através do balanceamento dessa equação de combustão!
Pra quantidade de carbono ficar balanceada, a quantidade de do lado esquerdo deve ser igual à quantidade de do lado direito. Por isso, de dos reagentes deve ser igual a de dos produtos.
A quantidade de de é encontrada através do balanço de hidrogênio . Para a quantidade de ficar balanceada, os de dos reagentes devem ser iguais aos de dos produtos.
O coeficiente pode ser encontrado fazendo o balanço de oxigênio . Pra isso, os de presentes nos reagentes têm que ser iguais aos de dos produtos.
Substituindo na fórmula de :
Beleza, achamos o ar teórico ! Pra usar e encontrar o coeficiente , nós temos que usar um dado importante da questão! Veremos isso no próximo passo!
Passo 4
A questão nos informou que a combustão foi feita com de ar teórico. Com essa informação, somos capazes de achar a quantidade de ar usado na combustão.
Agora que vem o pulo do gato! Vamos usar a fórmula de pra achar o coeficiente !
Aeeee! Achamos o coeficiente da equação que queremos balancear! Agora nos resta calcular os outros coeficientes no próximo passo!
Passo 5
Substituindo o coeficiente na equação de combustão, encontramos:
Achamos o coeficiente , balanceando a quantidade de carbono dessa equação. Para a quantidade de ficar balanceada, de dos reagentes deve ser igual a de dos produtos.
Calculamos o coeficiente através do balanço de hidrogênio ! De acordo com esse balanço, os de dos reagentes precisam ser iguais aos de dos produtos.
Eba! Já achamos um dos termos que precisamos pra calcular ! Mas vamos continuar a achar os coeficientes, porque eles serão importantes no futuro!
Balanceando a quantidade de nitrogênio , conseguimos achar o coeficiente . Os de dos reagentes devem ser iguais aos de dos produtos.
Com o balnço de oxigênio , achamos o último coeficiente . Os de dos reagentes devem ser iguais aos de dos produtos.
Agora só resta achar no próximo passo pra poder cacular !
Passo 6
Quando o vapor d’água do produto começa a condensar a , sua pressão parcial fica igual à pressão de saturação da água a . Essa pressão pode ser encontrada na tabela termodinâmica de saturação da água como mostrado abaixo.
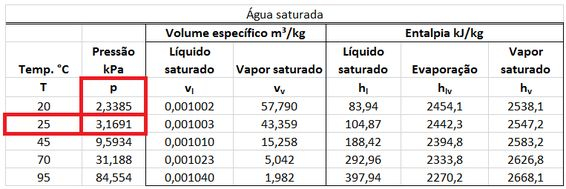
Se a gente dividir essa pressão parcial do vapor que está começando a condensar pela pressão total dos produtos , acharemos a fração de água no produto!
Cuidado! Não confunda com ! Calcular vai ser fundamental pra achar e . Existe outra forma de calcular a fração molar do vapor d’água nos produtos. Pra isso, nós dividimos a quantidade de de vapor d’água que ainda não foi condensada pela quantidade total de produtos que ainda não foram condensados.
A quantidade de de vapor d’água que ainda não foi condensada é igual à quantidade total de água nos produtos menos a quantidade de vapor que foi condensada .
Já a quantidade total de dos produtos que ainda não foram condensados é igual à quantidade total de produtos (soma de todos os coeficientes dos produtos) menos .
Susbtituindo os dados que temos:
Reorganizando essa equação, achamos o valor de .
Substituindo esse valor na fórmula de , achamos:
Prooooonto! Chegamos ao final desse exercício! Esse deu trabalho, né?
Resposta
Exercício Resolvido #7
Elaboração própria
de um carvão com análise final (em massa) corresponde a de , de , de , de , de e de cinzas não combustíveis é queimado completamente com de excesso de ar. Determine a equação balanceada dessa combustão.
Passo 1
Fala! Tudo bem com você? Vamos treinar um pouco seus conhecimentos de combustão?

O primeiro passo de qualquer exercício de combustão é escrever a equação da reação. O enunciado diz que o combustível passa por uma combustão completa com excesso de ar. Logo, , , e são os produtos. A questão também diz que , , , e reagem com o e o do ar. , , , e são os reagentes. Sabendo disso, escrevemos a equação:
, , , , , , , , , e são os coeficientes estequiométricos da equação química!
As cinzas não estão nessa equação, porque não participam da reação!
Fazer o balanceamento da equação é a mesma coisa que achar o valor desses coeficientes.

No entanto, para calcular todos esses coeficientes, precisamos descobrir quanto vale a quantidade de ar teórico. é a quantidade de ar necessária pra fazer do combustível passar por uma combustão completa sem gerar nos produtos. Ou seja, é encontrada balanceando a equação de combustão abaixo.
onde , , , , e são os coeficientes estequiométricos da equação da combustão sem excesso de ar.
Como o ar é formado por e , pode ser obtido, somando a quantidade de de com a quantidade de de .
Vamos começar o exercício, calculando os coeficientes , , , e dos combustíveis no próximo passo.
Passo 2
O primeiro passo para fazer o balanço de uma equação, quando o enunciado nos dá as composições dos produtos e do combustível, é determinar os coeficientes de cada componente do combustível.

Calcularemos , lembrando que de combustível é queimado. Pra isso, achamos primeiro a massa de multiplicando pelos de no combustível.
Da mesma forma, achamos a massa de , multiplicando pelos de no combustível. A massa de é encontrada, multiplicando pelos de .
Fazemos o mesmo com e . Suas massas e são calculadas, multiplicando a massa de do combustível todo pelas suas porcentagens mássicas dadas pelo enunciado.
Agora, para achar a quantidade de de nos reagentes, dividimos pela massa molar do carbono que vale .
é encontrado, dividindo pela massa molar do hidrogênio que vale segundo as tabelas termodinâmicas de gases.
Encontramos a quantidade de de presente no combustível, dividindo pela massa molar do que vale .
Por fim, achamos e , dividindo e pelas massas molares de e de .
Agora, vamos aprender a encontrar o coeficiente nos próximos passos, usando a porcentagem de ar teórico que o enunciado informa!
Passo 3
Para calcular , precisamos descobrir quanto vale a quantidade de ar teórico. é a quantidade de ar necessária pra fazer os de combustível passar por uma combustão completa sem gerar nos produtos. Ou seja, é encontrada balanceando a equação de combustão abaixo.
Vamos calcular através do balanceamento dessa equação de combustão!
Pra quantidade de carbono ficar balanceada, a quantidade de do lado esquerdo deve ser igual à quantidade de do lado direito. Por isso, de dos reagentes deve ser igual a de dos produtos.
A quantidade de de é encontrada através do balanço de hidrogênio . Para a quantidade de ficar balanceada, os de dos reagentes devem ser iguais aos de dos produtos.
é encontrado através do balanço de . Os de dos reagentes precisam ser iguais aos de dos produtos.
O coeficiente pode ser encontrado fazendo o balanço de oxigênio . Pra isso, os de presentes nos reagentes têm que ser iguais aos de dos produtos.
Substituindo na fórmula de :
Beleza, achamos o ar teórico ! Pra usar e encontrar o coeficiente , nós temos que usar um dado importante da questão! Veremos isso no próximo passo!
Passo 4
A questão nos informou que a combustão foi feita com de ar teórico. Com essa informação, somos capazes de achar a quantidade de ar usado na combustão.
Agora que vem o pulo do gato! Vamos usar a fórmula de pra achar o coeficiente !
Aeeee! Achamos o coeficiente da equação que queremos balancear! Agora nos resta calcular os outros coeficientes no próximo passo!
Passo 5
Só falta achar os coeficientes , , , e dos produtos. Achamos , fazendo o balanceamento de . Pra quantidade de carbono ficar balanceada, , de dos reagentes deve ser igual a de dos produtos.
A quantidade de de é encontrada através do balanço de hidrogênio . Para a quantidade de ficar balanceada, os de dos reagentes devem ser iguais aos de dos produtos.
é encontrado através do balanço de . Os de dos reagentes precisam ser iguais aos de dos produtos.
é encontrado pelo balanço de . Os de dos reagentes são iguais aos de dos produtos.
Por fim, achamos , balanceando a quantidade de oxigênio . Pra quantidade de ficar balanceada, os de presentes nos reagentes têm que ser iguais aos de dos produtos.
Aeeee! Achamos todos os coeficientes! Suamos, choramos, mas conseguimos!
Resposta
Exercício Resolvido #8
Elaboração própria
Uma amostra seca de carvão apresenta a seguinte análise mássica de: de carbono , de hidrogênio , de oxigênio , de nitrogênio , de enxofre e o restante de cinzas não combustíveis.
Admita que a amostra deste carvão é queimada com ar seco, gerando produtos com análise molar seca de de , de e de .
Determine a porcentagem de ar teórico dessa combustão.
Passo 1
Oie, galera! Esse enunciado é cheio de informação, né? Então vamos entender primeiro quais são os reagentes e produtos dessa combustão. Esse é sempre um bom início! Então partiu começar a questão!

O enuciado diz que , , , e reagem com ar seco que é composto por uma parte de e partes de . Como essas moléculas reagem, elas são os reagentes, certo?
O enunciado também diz que , , e são produzidos pela reação. Logo, essas moléculas são os produtos. Colocando os reagentes na esquerda e produtos na direita:
, , , , , , , , e são os coeficientes estequiométricos da equação química!
As cinzas não estão nessa equação, porque não participam da reação!
Esses coeficientes estequiométricos precisam ser encontrados para encontrarmos a porcentagem de ar teórico que o enunciado pede. A fórmula dessa porcentagem é:
é a quantidade de de ar usado na combustão e é a quantidade de de ar teórico. é encontrada a partir da equação da combustão que o enunciado cita.
Vamos começar a fazer as contas, calculando , , , e . Esses coeficientes serão importantes pra achar e .
Passo 2
Pra achar , , , e , temos que fazer o balanço da equação de combustão. O primeiro passo para fazer o balanço de uma equação, quando o enunciado nos dá as composições dos produtos e do combustível, é determinar os coeficientes de cada componente do combustível.

Calcularemos , supondo que de combustível é queimado. Pra isso, achamos primeiro a massa de multiplicando pelos de no combustível.
Da mesma forma, achamos a massa de , multiplicando pelos de no combustível. A massa de é encontrada, multiplicando pelos de .
Fazemos o mesmo com e . Suas massas e são calculadas, multiplicando a massa de do combustível todo pelas suas porcentagens mássicas dadas pelo enunciado.
Nós calculamos as massas pro caso de de combustível serem queimados, mas poderia ser qualquer quantidade de combustível! Esse valor não interfere no cálculo do ar teórico!
Agora, para achar a quantidade de de nos reagentes, dividimos pela massa molar do carbono que vale .
é encontrado, dividindo pela massa molar do hidrogênio que vale segundo as tabelas termodinâmicas de gases.
Encontramos a quantidade de de presente no combustível, dividindo pela massa molar do que vale .
Por fim, achamos e , dividindo e pelas massas molares de e de .
Com esses coeficientes já somos capazes de achar os coeficientes restantes!
Passo 3
Para achar os coeficientes dos produtos, consideramos que de combustível gera uma quantidade desconhecida de produtos.
Dessa forma, achamos o coeficiente do , multiplicando pelos de .
O coeficiente de é encontrado de forma bem parecida! Pra encontrar , multiplicamos a quantidade de produtos secos pela porcentagem de presente nos produtos secos!
Por fim, encontramos o coeficiente de , multiplicando os de produtos secos pela porcentagem de presente nesses produtos.
Agora, falta achar e os coeficientes estequiométricos e que faltam no próximo passo.
Passo 4
Pra achar o valor de produtos secos gerados na combustão de de combustível, balanceamos a quantidade de carbono da equação abaixo. A equação abaixo mostra os coeficientes já calculados. Como , e estão em função de , colocamos o em evidência!
![]()
Pra balancear , os de presentes presente nos reagentes precisam ser iguais aos de dos produtos. Logo:
Agora resta achar e !
Pra achar , fazemos o balanço do hidrogênio . Esse balanço nos diz que a quantidade de de dos reagentes deve ser igual à quantidade de dos produtos!
Calcularemos o coeficiente , usando o balanço de oxigênio !
O balanço de oxigênio diz que de dos reagentes devem ser iguais a de presente nos produtos.
Agora sim estamos aptos a calcular ! Vamos aprender a calcular e no próximo passo.
Passo 5
Como o ar seco é formado por e , achamos a quantidade de de ar, somando a quantidade de de com a quantidade de de .
Como é a quantidade de ar necessária pra fazer o carbono passar por uma combustão completa sem gerar nos produtos, é encontrada balanceando a equação de combustão abaixo.
onde , , , , e são os coeficientes estequiométricos da equação da combustão sem excesso de ar.
Como o ar é formado por e , pode ser obtido, somando a quantidade de de com a quantidade de de .
Vamos começar a achar esses coeficientes pra encontrar no próximo passo.
Passo 6
Pra quantidade de carbono ficar balanceada, a quantidade de do lado esquerdo deve ser igual à quantidade de do lado direito. Por isso, de dos reagentes deve ser igual a de dos produtos.
A quantidade de de é encontrada através do balanço de hidrogênio . Para a quantidade de ficar balanceada, os de dos reagentes devem ser iguais aos de dos produtos.
é encontrado através do balanço de . Os de dos reagentes precisam ser iguais aos de dos produtos.
O coeficiente pode ser encontrado fazendo o balanço de oxigênio . Pra isso, os de presentes nos reagentes têm que ser iguais aos de dos produtos.
Substituindo na fórmula de :
Susbtituindo e na fórmula de porcentagem de ar teórico:
Que coisa boa! Já chegamos ao final desse exercício! Tudo que é bom passa rápido, né?