Propriedades de misturas e fugacidade
Produzido por Philip Canabarro BlockerTeoria
Variação de entropia para uma mistura
No capítulo anterior vimos como funciona a variação de diversas propriedades no caso de uma mistura, vimos também que a entropia não funciona do jeito convencional. Vamos supor que duas substâncias e se misturem num processo adiabático e que não há variação de volume, pressão ou temperatura e onde é a pressão parcial do componente e a pressão parcial do componente .
Assim como para as propriedades vistas no capítulo anterior vamos ter que a variação da entropia na mistura será
A variação de entropia de um componente já foi mostrada no capítulo “Outras relações termodinâmicas” e é dada por
De forma análoga para
Logo, a variação total de entropia será
Olha só que interessante, o aumento da entropia depende apenas do número de mols! Podemos, também, fazer uma equação geral, para mais de duas substâncias.
Compressibilidade
Antes de falar mais sobre o conceito de misturas é importante saber o que é a compressibilidade de um gás. Compressibilidade é uma grandeza que mede o quanto um gás real difere de um gás ideal, é representada pela letra e calculada como:
Observe que quando o gás se comporta como um gás ideal. Isso acontece em algumas condições e alguns exemplos são:
- Quando a pressão tende a zero.
- Em temperaturas da ordem de 300K (temperatura ambiente) e superiores; e pressões até 10 MPa.
Mas porque essa grandeza chama-se compressibilidade?
Vamos supor um gás a temperatura de 300K e pressão de 4MPa (dentro do nosso segundo exemplo, descrito acima) ao abaixarmos a temperatura as moléculas se aproximarão e começarão a interagir com forças de atração intermoleculares. Com isso, a massa específica (que é o inverso do volume específico) irá aumentar, assim, a massa específica real se torna maior do que a massa específica dada pela equação dos gases perfeitos e, portanto, .
Isso pode ocorrer de forma análoga, quando em elevadas pressões vamos ter . Por isso, essa grandeza é chamada de compressibilidade, pois calcula a variação da massa específica e proximidade entre as moléculas em comparação com a equação dos gases perfeitos.
Fugacidade
Acabamos de ver o conceito de compressibilidade e uma forma de relacionar gases reais com gases perfeitos. A fugacidade faz mais ou menos a mesma coisa, mas com a pressão. Ou seja, a fugacidade é como se fosse uma pressão e, quando utilizada no lugar da pressão de fato, podemos utilizar as mesmas equações que normalmente usamos para os gases perfeitos.
Além disso, a fugacidade mantém uma relação bem próxima com a função de Gibbs (). Na verdade o conceito de fugacidade vem da relação de Gibbs. Relembrando:
Caso tenhamos uma transformação isotérmica então a equação se reduz a
Para um gás real e utilizando o conceito de compressibilidade apresentado anteriormente vamos ter
Essa identidade acontece porque o segundo e terceiro termos são iguais:
Então podemos definir a fugacidade como:
Perceba que a compressibilidade foi retirada e a fugacidade implementada no lugar da pressão. Outra coisa importante também é o fato de a baixas pressões a fugacidade se aproximar da pressão (porque um gás a baixas temperaturas se aproxima de um gás perfeito), assim teremos a restrição:
Podemos ir um pouco mais além e achar uma relação entre a variação da função de Gibbs e a fugacidade e pressão, isso pode ser feito integrando a equação ao longo de uma isotérmica desde uma pressão muito baixa até uma pressão qualquer, obtendo.
Caso fosse um gás perfeito o resultado seria da forma
Se subtrairmos uma equação da outra e utilizarmos a relação de Gibbs
Vamos ter
Essa equação parece ser bem difícil de entender não é mesmo? Mas todos esses termos são tabelados o que facilita muito o uso dessa equação, os termos tabelados são
- Entalpia residual
- Entropia residual
- Temperatura relativa
- Temperatura crítica
- Coeficiente de fugacidade
O coeficiente de fugacidade, assim como todas essas outras grandezas, é tabelado mas também pode ser obtido através da relação:
Fugacidade para misturas
Show de bola, isso tudo foi para definir a fugacidade para uma substância simples. Como fica então a fugacidade para uma mistura de substâncias?
A fugacidade da substância de uma mistura pode ser dada por
Agora a restrição leva em consideração a fração molar do componente .
Compressibilidade
Fugacidade
Fugacidade para misturas
Exercícios Resolvidos
Exercício Resolvido #1
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentals of Thermodynamicas, 6ª ed. americana. 2002, Exercício 12.6
Dois fluxos dos gases A e B são misturados numa proporção molar de 1:1 ambos a mesma temperatura. Qual é a geração de entropia por kmol no fluxo de saída?
Passo 1
Da teoria sabemos que a geração de entropia em misturas acontece da forma:
Como a mistura é de 1:1 em mols, então temos que e assim como e . Dessa forma obtemos:
Resposta
Exercício Resolvido #2
Elaboração própria
Considerando a grandeza denominada compressibilidade dada por
O que significa quando um gás possui e quando ?
Passo 1
A compressibilidade é a grandeza que mede o quanto um gás real difere de um gás perfeito. Quando a compressibilidade é igual a 1 então trata-se de um gás perfeito.
Quando isso significa que
Ou seja, a pressão vezes o volume específico será maior do que para um gás perfeito. Como a pressão é um fator externo então a mudança no gás ocorre no próprio volume específico – que fica maior – Como o volume específico é o inverso da massa específica
Vamos ter que a massa específica fica menor, logo, quando o gás real se torna menos denso do que o gás ideal.
Quando o oposto ocorre e o gás se torna mais denso do que o gás perfeito.
Passo 2
Essa diferença entre o real e o ideal ocorre devido às interações moleculares do gás. Quando as moléculas estão a uma certa distância existem forças de atração intermoleculares (caso e se continuarmos aproximando as moléculas elas vão estar tão próximas que a força intermolecular será de repulsão (caso )
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
Elaboração própria
Sabendo que o coeficiente de fugacidade
É um termo tabelado e num dado processo em que a pressão inicia em 100kPa e vai até 5MPa e o coeficiente de fugacidade varia de -0,03 até -0,77 calcule a fugacidade no início e no fim do processo. É possível calcular o trabalho a partir da fugacidade?
Passo 1
A primeira parte desse exercício consiste apenas em substituir os valores de pressão e igualar ao coeficiente de fugacidade. Para o início do processo temos:
Para o final do processo
Passo 2
A fugacidade está intimamente ligada à função de Gibbs da forma
Ou seja, no caso de um processo no qual a função de Gibbs possa ser utilizada para calcular o trabalho então sim é possível calcular o trabalho a partir da fugacidade.
Resposta
Exercício Resolvido #4
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentals of Thermodynamicas, 6ª ed. americana. 2002, Exercício 12.7
Um container rígido possui 1 kg de argônio a 300K e 1 kg de argônio a 400K ambos a 150kPa. Eles são misturados sem que haja calor externo envolvido. Qual a temperatura e a pressão final? Existe geração de entropia? Dado:
Passo 1
Esse exemplo trata de uma mistura de um mesmo elemento a diferentes temperaturas. É importante perceber que não há trabalho ou calor externo, portanto, a energia interna se conserva. Além disso, o container é rígido, ou seja, o volume também se conserva.
Com essas duas informações podemos utilizar as equações dos gases e achar a temperatura e a pressão final.
Passo 2
A variação da energia é definida como
Neste caso e considerando a temperatura final da mistura teremos
O que faz bastante sentido já que temos uma mistura 1:1 de um mesmo gás.
Passo 3
Agora podemos utilizar a equação dos gases perfeitos para achar a pressão.
Com a pressão final a temperatura final e a massa igual a 2 kg.
Como não temos o volume inicial temos de aplicar a equação novamente para os dois componentes.
Somando os dois obtemos
Como , temos que
Agora podemos utilizar a primeira equação
Passo 4
A geração de entropia acontecerá devido à mistura das temperaturas apenas e como descrita no capítulo “Outras relações termodinâmicas” pode ser expressa como:
Resposta
Exercício Resolvido #5
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentals of Thermodynamicas, 6ª ed. americana. 2002, Exercício 12.59
Um fluxo de 2 kg/s de uma mistura 50% e 50% em massa é aquecida a pressão constante de 400K para 1000K por uma fonte de radiação a 1400K. Ache a taxa de transferência de calor e a entropia gerada no processo.
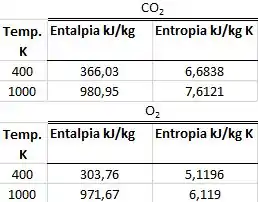
Passo 1
Como não há trabalho envolvido nesse sistema temos que a transferência de calor será igual a variação da entalpia:
Expandindo essa equação ficará da forma
Passo 2
Para a entropia temos que
Expandindo como fizemos com o calor fica da forma
Substituindo os valores
Resposta
Exercício Resolvido #6
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentals of Thermodynamicas, 6ª ed. americana. 2002, Exercício 12.46
Uma mistura de 0,5 kg de nitrogênio e 0,5 kg de oxigênio a 100 kPa e 300K é mantida num cilindro com pistão a pressão constante. Posteriormente 800 kJ de calor são adicionados. Ache a temperatura final e o incremento de entropia do sistema. Dados: ; .
Passo 1
Vamos atacar esse problema utilizando a primeira lei da termodinâmica:
O calor sabemos que é igual a 800 kJ.
O trabalho, por se tratar de um processo isobárico, será dado por
E a energia interna pode ser expressa como função da energia interna específica
Então a equação da primeira lei fica da forma:
Como a entalpia é igual a
Então podemos expressar o lado esquerdo dessa equação em função da entalpia
A entalpia também pode ser calculada como
Logo,
Passo 2
Até aqui estávamos fazendo uma análise como se não existisse mistura, mas é evidente que o será algum tipo de média entre o do nitrogênio e do oxigênio. Mais precisamente será uma média ponderada pela massa da forma:
Substituindo os valores fornecidos:
Com o valor de podemos voltar a tratar o problema como se não fosse uma mistura, assim:
Passo 3
Como a variação da entropia depende da temperatura e da pressão vamos ter que
Porém a pressão é constante logo
Substituindo temos
Resposta
Exercício Resolvido #7
Unicamp, Aula 21, propriedades de misturas parte 2, p. 15 (adaptada)
Uma mistura de 0,3 kg de CO2 e 0,2 kg de N2 é comprimida de 1 bar e 300 K a 3 bars seguindo um processo politrópico para o qual n=1,25. Determine:
a) a temperatura final.
b) o trabalho.
c) Encontre uma forma de calcular a transferência de calor.
d) Encontre uma forma de calcular a variação de entropia da mistura.
Passo 1
Para começar esse exercício é importante lembrar que um processo politrópico é definido da forma
Então iremos utilizar equações muito parecidas com as de um processo isentrópico, porém, ao invés de utilizar utilizaremos .
Passo 2
A temperatura pode ser calculada através da relação
Substituindo os valores temos
Passo 3
Vamos calcular o trabalho, para isso vamos começar com a definição de trabalho
Da equação dos gases temos que
Substituindo na equação do trabalho
A massa é igual a soma das massas dos dois componentes
A massa molecular da mistura é igual a massa total dividido pela soma do número de mols de cada substância
Agora é só substituir na equação
Passo 4
Para achar a transferência de calor vamos utilizar a primeira lei da termodinâmica:
Se acharmos o vamos saber a quantidade de calor trocado.
Como temos o número de mols de nitrogênio e gás carbônico, assim como as temperaturas final e inicial basta saber a energia interna de cada componente. A energia interna é tabelada então o que temos já basta para achar a variação de energia interna total e, consequentemente, o calor.
Passo 5
A variação de entropia da mistura segue uma lógica parecida com a variação da energia interna:
mas temos de lembrar que a variação da entropia ocorre da forma:
Isso para cada componente.
E aqui as entropias molares dos componentes também são propriedades tabeladas, como sabemos as temperaturas e pressões então o problema já esta fechado.
Resposta
Exercício Resolvido #8
Unicamp, Aula 21, propriedades de misturas parte 2, p. 24
2 tanques rígidos e isolados estão conectados por uma válvula. Inicialmente, tem-se 0,79 kmol de N2 a 2 bars e 250K em um dos tanques. O outro tanque contém 0,21 kmol de O2 a 1 bar e 300K. A válvula é aberta e um processo de mistura sem troca de calor ou trabalho com o ambiente externo ao tanque acontece, até que um estado de equilíbrio é atingido.
Dados: ;
Passo 1
Primeiro vamos calcular a temperatura final da mistura pela variação da energia interna, que é função apenas da temperatura. Como não há trabalho nem calor externo então temos que a energia interna do sistema permanece a mesma: .
A energia interna de um gás () numa mistura pode ser dada em função do número de mols , a temperatura e a energia interna molar desse gás (). Logo
Como
obs: Aqui a temperatura não está sendo multiplicada pela energia interna, ao invés disso, indica apenas em qual temperatura aquela energia interna está sendo avaliada (como se fosse uma função, até porque de fato a energia interna é função da temperatura).
lembrando que a energia interna específica molar é dada por
Vamos ter
obs: Agora a temperatura está de fato sendo multiplicada pelo .
Dessa forma podemos isolar que é a temperatura final e obtemos:
Passo 2
Agora vamos substituir os dados da questão:
Passo 3
Agora vamos calcular a pressão final da mistura. Vamos fazer isso utilizando a equação geral dos gases perfeitos.
O pulo do gato aqui é lembrar que o volume da mistura é a soma dos volumes antes da mistura, isolando o volume para cada gás vamos ter
Para o oxigênio
Agora voltamos à equação dos gases para o estado final, que fica da forma:
Passo 4
Por fim iremos calcular a geração de entropia, que é dada por:
Para relembrar temos que, num processo reversível, a variação de entropia é
Mas esse processo não é reversível por isso adicionamos o termo de geração de entropia .
Como o processo é adiabático então a variação de entropia é igual a própria geração
A variação de entropia da mistura segue uma lógica parecida com a variação da energia interna:
Passo 5
Vamos calcular a entropia antes e depois sabendo que a entropia será função da temperatura e da pressão, dessa forma temos que:
Para o nitrogênio será:
para o oxigênio
portanto a geração será a soma