Teoria
O que é energia interna ?
Quando a gente realiza trabalho para comprimir uma mola, energia potencial elástica é armazenada no interior dela. Quando um peso é levantado até uma altura, energia potencial gravitacional é armazenada dentro dele. Que tipo de energia é armazenada em um sistema, quando a gente comprime a sua fronteira ou fornece calor para ele?
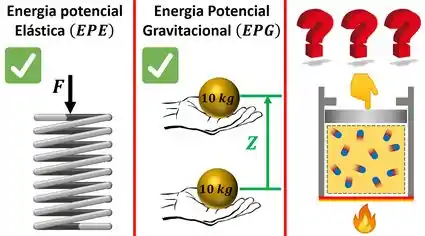
A energia interna do sistema! Ou seja, quando a vizinhança realiza trabalho sobre o sistema ou dá calor pra ele , a energia interna do sistema aumenta.
Ela é armazenada de várias formas dentro do sistema. Aumentando a energia cinética das moléculas, se acumulando nas ligações entre as moléculas, se acumulando nas ligações químicas entre os átomos que formam as moléculas e se acumulando dentro dos átomos!
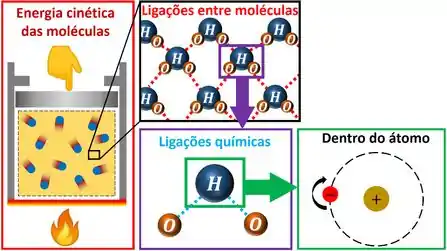
Como energia interna é uma forma de energia, a sua unidade no Sistema Internacional (S.I.) é o joule . Mas é muito comum ela aparecer em quilojoule nos exercícios!
Por que a energia interna é tão importante?
Agora a gente já conhece algumas informações sobre a energia interna! Mas mesmo assim ainda fica uma dúvida: qual a importância de saber tudo isso sobre uma forma de energia?
Ela é importante, porque é uma propriedade extensiva do sistema muito comum de aparecer em questões de termodinâmica!
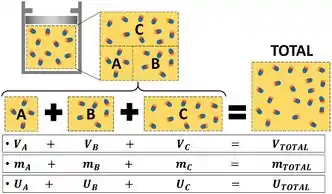
Isso significa que o valor da energia interna total de um sistema é igual à soma do valor das energias internas de cada parte desse sistema, como mostrado na figura!
Para entender melhor isso, vamos fazer um exercício!

Qual é a energia interna total de um sistema formado por água líquida saturada com de energia interna e por vapor d’água saturado com ?
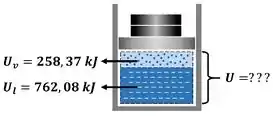
Como foi dito antes, a energia interna total é a soma da energia interna das partes ( e ).
A energia interna total do sistema vale . Esse exercício ensinou pra gente duas coisas: como calcular a energia interna total do sistema, sabendo as energias internas das partes e como calcular a energia interna total de uma mistura de líquido saturado com vapor saturado! A fórmula dessa energia interna total da mistura bifásica saturada é:
onde:
- é a energia interna do líquido saturado;
- é a energia interna do vapor saturado.
Energia interna específica
A gente precisa do valor de apenas duas propriedades intensivas independentes para determinar o valor de todas as outras propriedades e definir um estado termodinâmico. O problema é que a energia interna é uma propriedade extensiva. Ela não pode ser usada pra fixar o estado! Isso quer dizer que ela é totalmente inútil para definir um estado?!

Não, porque existe uma forma de criar uma propriedade intensiva a partir da energia interna! Aí a gente poderia usar essa nova propriedade para determinar o valor de todas as outras. Ou seja, essa nova propriedade é mais uma informação que podemos usar nos exercícios para definir o estado de um sistema! Ela se chama energia interna específica. Sua fórmula é:
onde:
- é a energia interna específica. Sua unidade no Sistema Internacional (S.I.) é joule por quilograma . No entanto, nas tabelas de propriedade, ela aparece em quilojoule por quilo ;
- é a energia interna do sistema;
- é a massa do sistema. Ela é medida em quilograma de acordo com o S.I.
Vendo essa fórmula, qual seria a energia interna específica de de água líquida com de energia interna acumulada no seu interior? Descobrimos o resultado, aplicando a fórmula:
Energia interna específica de uma mistura bifásica
Com o exemplo anterior, descobrimos como podemos calcular a energia interna específica de um sistema formado por uma única fase! No caso resolvido, a fase era líquida. Mas como podemos calcular a energia interna específica de um sistema formado por uma parte de líquido saturado e outra de vapor saturado? Usando a mesma fórmula:
sendo a massa total do sistema.
Só que no caso da mistura, a energia interna total é igual à energia interna do liquido saturado mais a energia interna do vapor saturado . Sabendo disso, a fórmula vira:
A energia interna de cada fase ( e ) pode ser encontrada, reorganizando a fórmula de energia interna específica do líquido e a fórmula de energia interna específica do vapor .
onde é a massa da parte líquida e é a massa do vapor.
Substituindo essas expressões de energia interna na fórmula de energia interna específica média , temos que:
Para chegar em uma equação que depende do título da mistura, temos que lembrar que:
Usando essa informação, chegamos na fórmula final de energia interna específica para uma mistura de líquido saturado com vapor saturado.
Como descobrir os valores de e ?
Chegamos em uma fórmula de energia interna específica para uma mistura saturada, depois de suar muito! Mas como a gente consegue usar essa fórmula, se nós ainda não sabemos onde achar os valores de e ? Aí complica, né?! Calma, que esses dois valores estão em tabelas de propriedades para substância saturada!
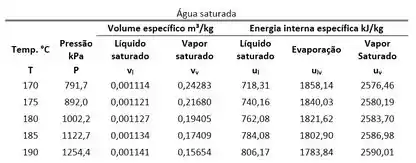
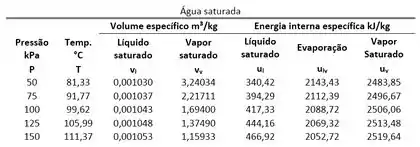
As tabelas acima mostram o valor de e da água. A de cima é usada, quando a gente sabe a temperatura da água saturada. A de baixo é usada, quando a gente conhece a pressão da água saturada. Ou seja, se a pressão da mistura saturada de água for igual a :
Se a temperatura da mistura saturada de água for igual a , e valem:
Essas tabelas têm tanta informação, que têm até um esquisito bem no meio de e . O que é isso? Essa variável é só a diferença entre e .
Como determinar outras propriedades, conhecendo a energia interna específica ?
Foi dito que se a gente soubesse os valores de duas propriedades intensivas independentes, a gente conseguiria determinar o valor de todas as outras propriedades intensivas do sistema. Então como a gente encontra os valores dessas propriedades restantes, conhecendo o valor da energia interna específica do sistema? Usando as tabelas de propriedades!
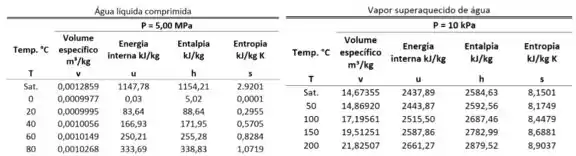
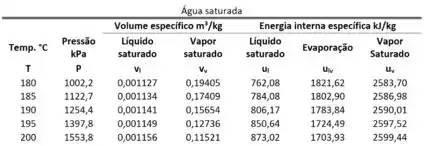
Como podemos ver pela figura acima, existem três tabelas muito comuns em questões de termodinâmica: uma tabela de líquido comprimido, uma tabela de saturação e uma tabela de vapor superaquecido. Como podemos descobrir qual delas devemos usar? Comparando o valor de dado com os valores de e !
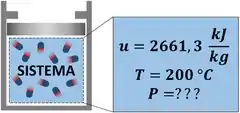
A imagem acima mostra um sistema formado por água. Sabemos que ela está a e que a sua energia interna específica vale , qual é a sua pressão?
Para decidir qual tabela devemos usar, seguimos uma regra: se a energia interna específica for maior que a energia interna específica do vapor saturado a , usamos a tabela de vapor superaquecido.
Se for menor que a energia interna específica do líquido saturado a , usamos a tabela de líquido comprimido.
Por fim, se o valor de estiver entre e , usamos a tabela de saturação.
No nosso exemplo o valor para água a vale . Já o valor de é igual a . Ou seja:
Por causa disso, usaremos a tabela de vapor superaquecido. Nela, descobrimos que a pressão da água a e com de energia interna vale !
Pronto, encontramos uma propriedade, conhecendo os valores de apenas duas propriedades intensivas!
Energia interna específica u
Energia interna específica de uma mistura bifásica
Como descobrir os valores de u l e u v ?
Como determinar outras propriedades, conhecendo a energia interna específica u ?
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Determine a energia interna de um balde com de água líquida saturada à pressão atmosférica de . Use a tabela abaixo.
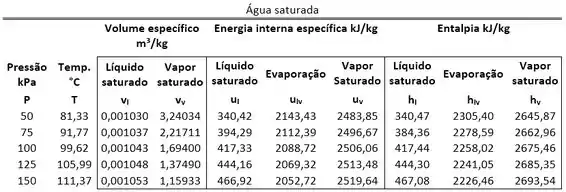
Passo 1
Devemos primeiro visualizar o exercício através da figura do balde de água líquida.
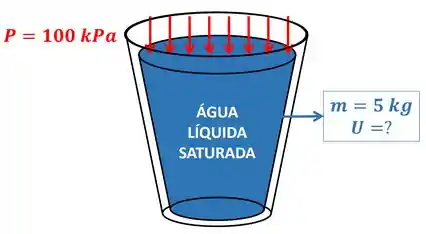
O enunciado pede para a gente encontrar a energia interna de de água líquida saturada, mas a tabela que ele nos deu tem apenas valores de energia interna específica . Como podemos resolver esse impasse? Lembrando da fórmula da energia interna em função da energia interna específica.
Essa fórmula mostra pra gente que para encontrar só precisamos multiplicar pela massa do sistema! Então quanto valem e ? Começando pelo , vemos que o valor de para líquido saturado está na mesma linha que a pressão de e na mesma coluna que .
A massa é informada pelo próprio enunciado:
Vamos encontrar na próxima etapa e depois vamos usar a fórmula para achar .
Passo 2
Como podemos extrair o da tabela? Lembrando que ele fica na mesma linha que a pressão da água e na mesma coluna que .
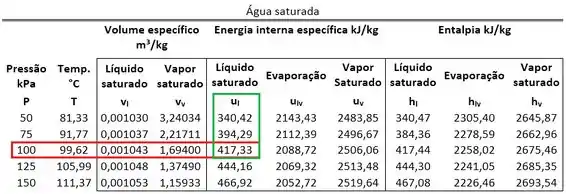
Então:
Sabendo disso, já podemos usar a fórmula de energia interna no próximo passo!
Passo 3
Esse é o resultado que queríamos!
Resposta
Exercício Resolvido #2
Elaboração própria
Um tanque rígido possui uma mistura de água líquida saturada com de vapor d’água saturado com um título de 0,4. Considerando que ambos estão a de pressão, determine a energia interna da mistura. Use a tabela abaixo.
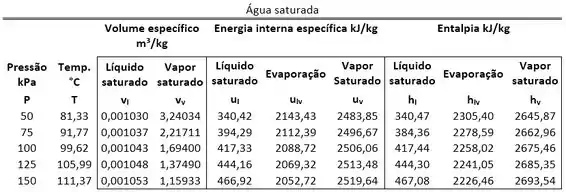
Passo 1
Devemos primeiro visualizar o exercício através da figura do tanque rígido com a mistura dentro.
O enunciado pede para a gente encontrar a energia interna total da mistura de água líquida saturada com vapor saturado d’água, mas a tabela que ele nos deu tem apenas valores de energia interna específica . Como podemos resolver esse impasse? Lembrando da fórmula da energia interna de líquido e vapor saturados em função das energias internas específicas.
Essa fórmula mostra pra gente que para encontrar só precisamos multiplicar pela massa do sistema! Então quanto valem e ? Os valores de e são extraídos das tabelas.
A massa de vapor é informada diretamente pelo enuciado.
Já a massa de líquido só pode ser calculada indiretamente:
A massa total da mistura pode ser descoberta pela fórmula do título.
Vamos encontrar e na próxima etapa e depois vamos usar as fórmulas para achar .
Passo 2
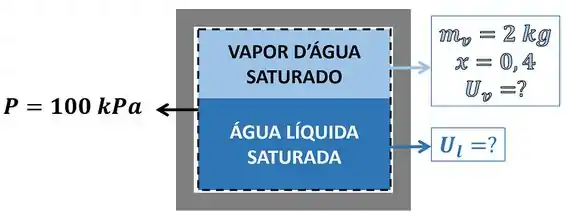
Como podemos extrair o da tabela? Lembrando que ele fica na mesma linha que a pressão da água e na mesma coluna que .
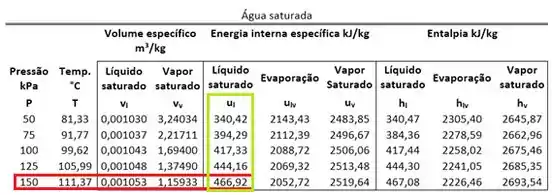
Então:
O é encontrado da mesma forma.
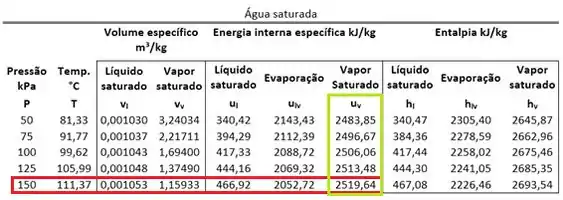
Sabendo disso, já podemos usar as fórmulas de energia interna no próximo passo!
Passo 3
Para o vapor saturado a equação é:
Para calcular a energia interna do líquido, precisamos primeiro calcular a massa de líquido e a massa total.
Agora sim usamos a fórmula de energia interna para o líquido.
A energia interna total é a soma das duas partes da mistura. Vapor e líquido.
Resposta
Exercício Resolvido #3
Elaboração própria
Determine se a água é um vapor superaquecido, um líquido comprimido ou se ela está saturada, usando a tabela de propriedades dada. Considere o seguinte caso:
, e .
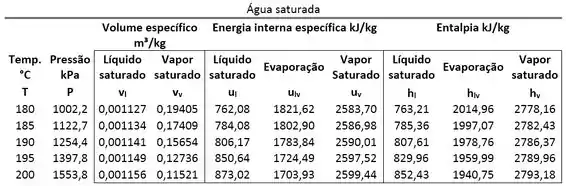
Passo 1
Para saber se a água está em uma dessas três opções. Devemos comparar sua energia interna específica com as energias internas específicas do vapor saturado e do líquido saturado .
O enunciado informa que:
Porém ele não informa diretamente. Para calculá-lo, precisamos lembrar que:
Temos todos esses valores. Agora é só aprender a descobrir a fase da água! Faremos isso na próxima etapa.
Passo 2
Agora vamos comparar esses valores com as condições de saturação da água informadas pela tabela!
Se a energia interna específica for maior que a energia interna específica do vapor saturado a , então a água é um vapor superaquecido.
Se for menor que a energia interna específica do líquido saturado a , a água é um líquido comprimido.
Por fim, se o valor de estiver entre e , a água está saturada.
Sabendo disso vamos achar as três energias internas (, e ) e fazer a comparação!
Passo 3
Vemos que para as energias internas do líquido saturado e vapor saturado são:
Podemos calcular achar a energia interna específica da água pela fórmula.
Comparando essa energia interna específica com as energias internas de saturação, vemos que:
Logo a água é um vapor superaquecido!
Resposta
A água é um vapor superaquecido.
Exercício Resolvido #4
Elaboração própria
Determine a energia interna específica da água, usando as tabelas de propriedades dada. Considere o seguinte caso:
, e .
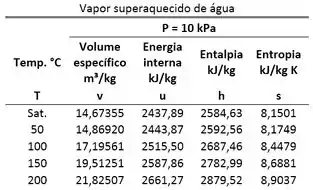
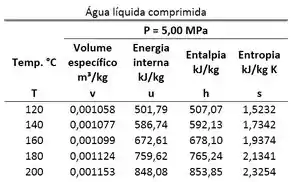
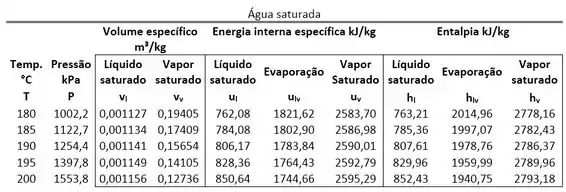
Passo 1
Primeiro, para saber qual tabela devemos usar, devemos comparar o volume específico da água com os volumes específicos do vapor saturado e do líquido saturado para temperatura igual a que estão na tabela de saturação.
O enunciado informa que:
Porém ele não informa diretamente. Para calculá-lo, precisamos lembrar que:
Temos todos esses valores. Agora é só aprender a descobrir a fase da água para determinar qual tabela vamos usar! Faremos isso na próxima etapa.
Passo 2
Agora vamos aprender a descobrir a fase da água, comparando o volume específico com os volumes específicos informados pela tabela !
Se volume específico for maior que volume específico do vapor saturado a , então a água é um vapor superaquecido e precisaremos usar a tabela de vapor superaquecido.
Se for menor que volume específico do líquido saturado a , a água é um líquido comprimido. Aí teremos que usar a tabela de líquido comprimido.
Por fim, se o valor de estiver entre e , a água está saturada.
Antes de comparar esses valores, precisamos entender a pegadinha dessa questão e alguns outros tópicos. É sobre isso que o próximo passo vai falar!
Passo 3
Atenção para a seguinte pegadinha! Ainda não sabemos se podemos usar as tabelas de vapor superaquecido e de líquido comprido, porque elas só podem ser usadas paras as pressões de e respectivamente e ainda não sabemos a pressão da água!

Além dessa pegadinha, devemos nos preocupar em achar o título da água, caso ela esteja saturada! Como podemos fazer isso? Reorganizando a fórmula de volume específico médio para mistura!
Só com esse valor que seremos capazes de calcular a energia interna específica da água caso ela seja uma mistura entre vapor e líquido. Quando ela for uma mistura saturada, a fórmula de energia interna específica vai precisar dessa variável.
Agora vamos encontar os três volumes específicos (, e ) e descobrir qual é a fase da água!
Passo 4
Vemos que para os volumes do líquido saturado e vapor saturado são:
Podemos calcular achar o volume específico da água pela fórmula.
Comparando esse volume específico com volumes específicos de saturação, vemos que:
Logo a água está saturada! Ou seja, precisaremos usar apenas a tabela de saturação para descobrir a sua energia interna específica. Como seu volume específico está entre os dois valores de saturação, sabemos também que ela é uma mistura saturada com o título valendo:
Ou seja, para calcularmos a sua energia interna específica temos que encontrar o valor do título. E é exatamente isso que faremos na próxima etapa!
Passo 5
Agora só falta obter os valores de energia interna específica saturada através da tabela para encontrarmos o resultado que queremos. Conseguimos cumprir esse passo, olhando para a tabela a seguir:
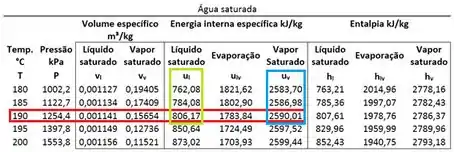
Substituindo esses valores na equação principal, alcançamos o resultado final:
Resposta
Exercício Resolvido #5
Elaboração própria
Conforme ilustrado na figura abaixo, um conjunto ciclindro-pistão contém de água a . O pistão está livre para mover-se suavemente no cilindro. A pressão atmosférica e a aceleração da gravidade são de e , respectivamente. Para a água, determine a pressão, em , e a energia interna, em joule . Use as tabelas de propriedades termodinâmicas abaixo.
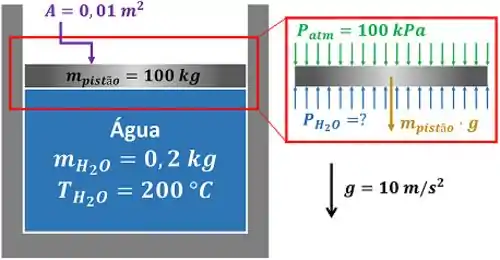
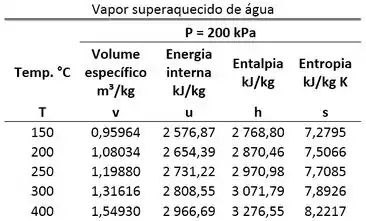
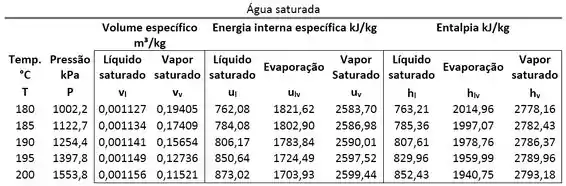
Passo 1
O primeiro passo para entender essa questão é saber como encontrar a pressão da água. Ela está sendo comprimida por duas coisas: pela atmosfera e pelo peso do pistão. A pressão que a atmosfera faz sobre a água já é dada pelo enunciado.
A pressão que o peso do pistão faz sobre a água é dada indiretamente pelo enunciado. Ela é igual ao peso do pistão dividido pela sua área .
A massa do pistão e a aceleração da gravidade também são informadas.
A pressão total exercida da água deve ser igual à soma dessas duas pressões.
Mas por que a pressão da água deve ser igualzinha á soma dessas duas pressões? Porque o enunciado informa que o pistão está livre para mover-se suavemente no cilindro. Isso significa que a água tem que sustentar o peso da atmosfera mais o peso do pistão para manter o pistão apoiado e equilibrado sobre ela!

Agora que sabemos como calcular a primeira incógnita que o enunciado pede, vamos aprender a calcular a próxima: e energia interna da água .
Passo 2
A primeira etapa para encontrar a energia interna da água é lembrar que ela é igual à energia interna específica vezes a massa da água.
A massa da água é dada diretamente pelo enunciado.
Já a energia interna específica é uma informação que precisamos descobrir através das tabelas de propriedades. O primeiro passo para achar esse valor é descobrindo se a água é um vapor superaquecido ou está saturada. Para saber isso, comparamos a pressão de saturação para a água a com sua pressão calculada no passo anterior.

Caso ela tenha pressão menor que a pressão de saturação, ela é um vapor superaquecido!
Caso ela tenha pressão igual à pressão de saturação, ela estará saturada.
Se ela for saturada, pegamos esse valor da tabela de saturação. Se ela for um vapor superaquecido, pegamos esse valor da tabela de vapor superaquecido.
Encontramos a sua energia interna específica na tabela através da sua pressão e da sua temperatura .
Agora que conhecemos todos os passos para chegar na resposta, vamos iniciar os cálculos!
Passo 3
Vamos começar as contas pela pressão que a massa do pistão exerce sobre a água .
Somando esse valor com a pressão atmosférica, achamos a pressão da água.
Agora vamos calcular a energia interna da água no próximo passo.
Passo 4
Para descobrir qual é o estado da água, comparamos a sua pressão com a pressão de saturação da água na temperatura de . Para saber qual é a pressão de saturação da água, usamos a tabela de saturação.
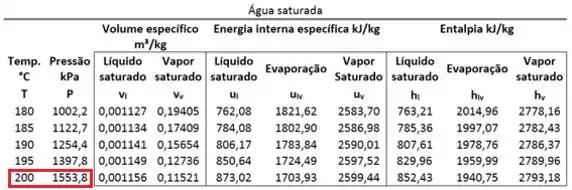
Logo, a pressão de saturação vale:
Ou seja:
A água é um vapor superaquecido. Então, devemos usar a tabela de vapor superaquecido para achar .
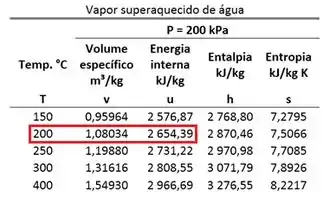
A energia interna específica da água vale:
Atenção, precisamos lembrar de converter a energia interna específica para joule por quilograma ! Como o exercício pede a energia interna da água em joule, essa conversão é necessária para a gente não se confundir depois.
Agora podemos achar a energia interna da água através da sua fórmula.
Pronto, encontramos as duas incógnitas que a questão pede!
Resposta
Exercício Resolvido #6
Elaboração própria
Amônia, inicialmente a e , é submetida a um processo sob volume específico constante até uma pressão final de . Determine, para o estado final, a energia interna específica. Use as tabelas abaixo.
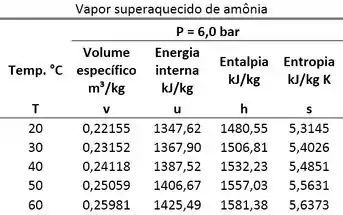
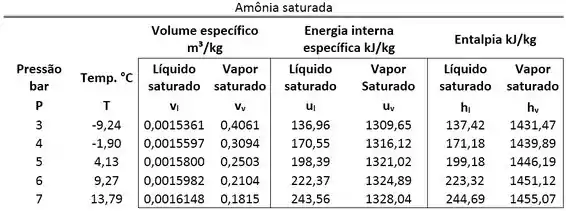
Passo 1
Esse exercício pede que a gente descubra o valor da energia interna específica da amônia, depois dela passar por um processo que mantém o seu volume específico igual. Ou seja, a amônia tinha um estado inicial (estado 1) e, depois de passar por esse processo, alcança seu estado final (estado 2). A figura abaixo mostra todas as informações dadas pelo enunciado.
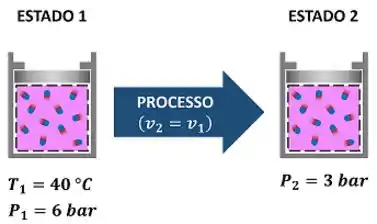
Como podemos achar a energia interna específica do estado 2 se nós só conhecemos o estado 1? Precisamos conhecer mais uma propriedade intensiva do estado 2 para fixarmos este estado e descobrirmos as suas propriedades intensivas restantes. Mas como faremos isso? Por enquanto só conhecemos a pressão desse estado .

Fazemos isso encontrando o valor de volume específico do estado 1 ! Como o processo mantém o volume específico da amônia igual:
Ou seja, dessa forma descobrimos mais uma propriedade intensiva do estado 2 e conseguimos fixar esse estado. A partir daí, achamos a energia interna específica através da tabela de propriedades!
Mas como encontramos o volume específico ?

Temos que descobrir se o estado 1 é saturado ou vapor superaquecido. Se o estado 1 for vapor superaquecido, usamos a tabela de vapor superaquecido. Se o estado 1 for saturado, usamos a tabela de vapor saturado para encontrar ! Para saber isso, comparamos a temperatura de saturação para a água a com sua temperatura .

Caso ela tenha temperatura maior que a temperatura de saturação, ela é um vapor superaquecido!
Caso ela tenha temperatura igual à temperatura de saturação, ela estará saturada.
Passo 2
Já sabemos como descobrir a fase do estado 1 comparando a sua temperatura com a temperatura de saturação . Como podemos descobrir a fase do estado 2, comparando o seu volume específico com os volumes específicos de saturação ( e )?

Se volume específico for maior que volume específico do vapor saturado a , então a amônia é um vapor superaquecido e precisaremos usar a tabela de vapor superaquecido.
Se o valor de estiver entre e , a amônia está saturada.
Se o estado 2 for vapor superaquecido, achamos a energia interna específica olhando a tabela de vapor superaquecido. E se o estado 2 for um estado saturado, como encontramos sua energia interna específica ? Usamos o ou o da tabela de saturação? Caso o estado 2 seja saturado, a energia interna específica tem a seguinte fórmula:
onde é o título do estado saturado 2.
Mas como podemos encontrar o valor de ? Se liga na dica: se queremos encontrar o título da mistura saturada e já sabemos o seu volume específico, podemos usar a fórmula a seguir:
onde é o volume específico do vapor saturado na pressão do estado 2 e é o volume específico do líquido saturado na pressão do estado 2 .
Pronto, agora que temos todas as informações que precisamos, vamos iniciar nossos cálculos.
Passo 3
Começamos as nossas contas, encontrando a temperatura de saturação do estado 1 para ver se esse estado é vapor superaquecido ou saturado. Pela tabela de saturação vemos que:
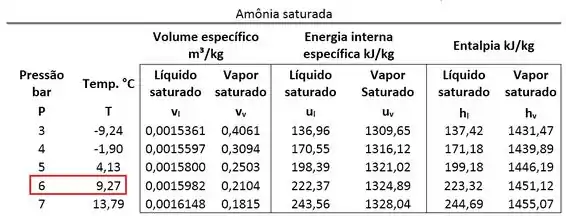
Como a temperatura do estado um vale , concluímos que:
O estado 1 é vapor superaquecido. Isso quer dizer que encontramos o volume específico desse estado olhando para a tabela de vapor superaquecido.
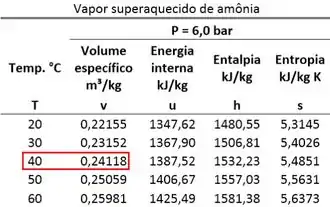
Como o volume específico do estado 2 é igual ao volume específico do estado 1, descobrimos que:
Ou seja, a pressão do estado 2 vale e o volume específico do estado 2 vale . Já fixamos este estado. Agora só falta saber qual é a fase do estado 2 para encontrarmos a sua energia interna específica .
Passo 4
Vemos pela tabela de saturação que os volumes específicos saturados valem:
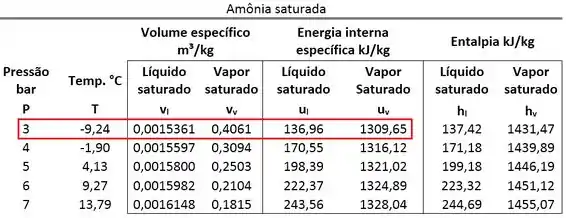
O volume específico do estado 2 está entre esses dois valores. Logo, o estado 2 é saturado. Então, para calcular temos que conhecer o título da mistura saturada.
Nessa tabela, também encontramos também os valores das energias internas de saturação que serão importantes para o cálculo de .
Substituindo esse valor na fórmula de :
Resposta
Exercício Resolvido #7
Elaboração própria
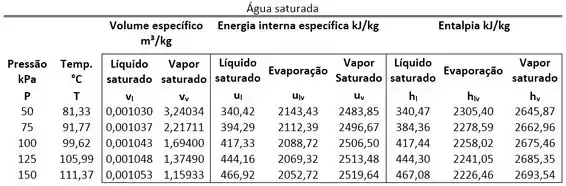
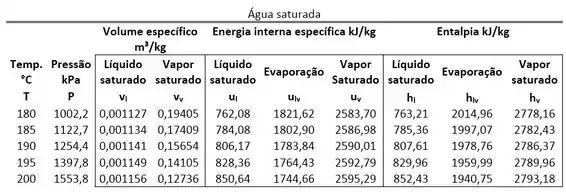
Um tanque rígido fechado contém água inicialmente como vapor saturado a , sendo esta resfriada até . Determine a energia interna final da água. Use as tabelas de propriedades abaixo.
Passo 1
Esse exercício pede que a gente descubra o valor da energia interna específica da água, depois dela passar por um processo. Ou seja, a água tinha um estado inicial (estado 1) e, depois de passar por esse processo, alcança seu estado final (estado 2). A figura abaixo mostra todas as informações dadas pelo enunciado.
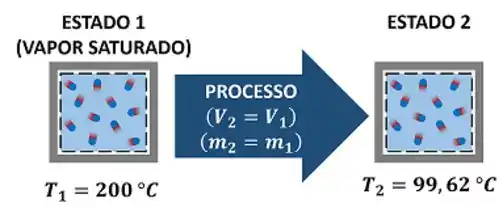
Como podemos achar a energia interna específica do estado 2 se nós só conhecemos o estado 1? Precisamos conhecer mais uma propriedade intensiva do estado 2 para fixarmos este estado e descobrirmos as suas propriedades intensivas restantes. Mas como faremos isso? Por enquanto, só conhecemos a temperatura desse estado .

Fazemos isso levando em conta algumas informações que estão escondidas no enunciado. A primeira delas é obtida, quando o enunciado fala que a água está contida em um tanque rígido. Se o tanque é rígido, ele permanece com o mesmo volume durante o processo. Ou seja, se o tanque é rígido, o volume que a água ocupa não muda.
A outra informação escondida é obtida na parte em que o enunciado diz que o tanque rígido está fechado. Isso significa que não tem massa de água entrando ou saindo do tanque. Logo, a massa de água não muda.
Como o volume e a massa da água permanecem iguais durante todo o processo, seu volume específico também permanece igual:
Ou seja, dessa forma descobrimos mais uma propriedade intensiva do estado 2 e conseguimos fixar esse estado. A partir daí, achamos a energia interna específica através da tabela de propriedades!
Mas como encontramos o volume específico ?

Através da tabela de saturação! Como o estado 1 é vapor d’água saturado, o volume específico é igual ao volume específico que está na linha da temperatura .
Passo 2
Já sabemos a fase do estado 1. Como podemos descobrir a fase do estado 2? Comparando o seu volume específico com os volumes específicos de saturação ( e )!
Se volume específico for maior que volume específico do vapor saturado a , então a amônia é um vapor superaquecido.
Se o valor de estiver entre e , a amônia está saturada.
Se o estado 2 for um estado saturado, como encontramos sua energia interna específica ? Usamos o ou o da tabela de saturação? Caso o estado 2 seja saturado, a energia interna específica tem a seguinte fórmula:
onde é o título do estado saturado 2.
Mas como podemos encontrar o valor de ? Se liga na dica: se queremos encontrar o título da mistura saturada e já sabemos o seu volume específico, podemos usar a fórmula a seguir:
onde é o volume específico do vapor saturado na temperatura do estado 2 e é o volume específico do líquido saturado na temperatura do estado 2 .
Pronto, agora que temos todas as informações que precisamos, vamos iniciar nossos cálculos.
Passo 3
Começamos as contas, encontrando o valor de na tabela de saturação. Antes, precisamos lembrar que o estado 1 é vapor saturado de água.
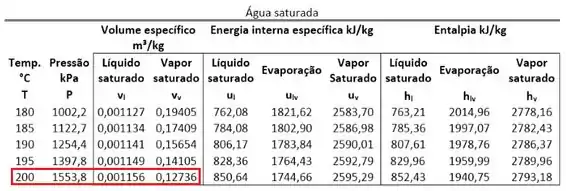
Como o volume específico do estado 2 é igual ao volume específico do estado 1:
Agora podemos comparar esse valor com os valores dos volumes específicos saturados para saber qual é a fase do estado 2. Para achar e usamos, de novo, a tabela de saturação.
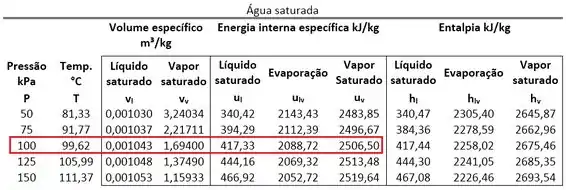
O volume específico do estado 2 está entre esses dois valores. Logo, o estado 2 é saturado. Então, para calcular temos que conhecer o título da mistura saturada. Faremos isso no próximo passo.
Passo 4
Nessa tabela, também encontramos também os valores das energias internas de saturação que serão importantes para o cálculo de .
Substituindo esse valor na fórmula de :
Resposta
Exercício Resolvido #8
Elaboração própria
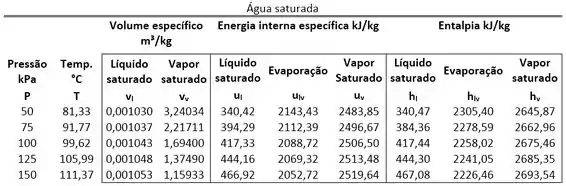
Um tanque rígido fechado, de de volume, contém água, inicialmente como uma mistura bifásica líquido-vapor a . A mistura é aquecida até um estado final, em que a temperatura é de e o título é de . Determine a energia interna do estado inicial da água. Use a tabela de propriedade abaixo.
Passo 1
Esse exercício pede que a gente descubra o valor da energia interna da água, antes dela passar por um processo de aquecimento. Ou seja, a água tinha um estado inicial (estado 1) e, depois do seu aquecimento, alcança seu estado final (estado 2). A figura abaixo mostra todas as informações dadas pelo enunciado.
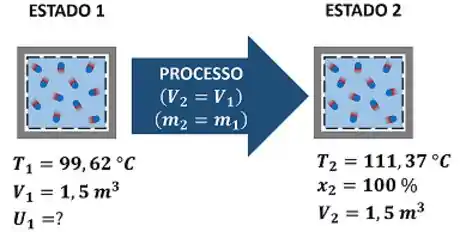
Como podemos achar a energia interna do estado 1 se nós só conhecemos o estado 2? Precisamos conhecer mais uma propriedade intensiva do estado 1 para fixarmos este estado e descobrimos as suas propriedades intensivas restantes. Com a energia interna específica , achamos através da fórmula:
onde é a massa de água do estado 1.
Mas como podemos fixar o estado 1 para achar e isso?
Por enquanto, só conhecemos a temperatura desse estado e o volume que a água ocupa .
Fazemos isso levando em conta algumas informações que estão escondidas no enunciado. A primeira delas é obtida, quando o enunciado fala que a água está contida em um tanque rígido. Se o tanque é rígido, ele permanece com o mesmo volume durante o aquecimento. Ou seja, se o tanque é rígido, o volume que a água ocupa não muda.
A outra informação escondida é obtida na parte em que o enunciado diz que o tanque rígido está fechado. Isso significa que não tem massa de água entrando ou saindo do tanque. Logo, a massa de água não muda.
Como o volume e a massa da água permanecem iguais durante todo o processo de aquecimento, seu volume específico também permanece igual:
Ou seja, o volume específico é mais uma propriedade intensiva desse estado e conseguimos fixar esse estado. A partir daí, achamos a energia interna específica através da tabela de propriedades!
Mas como encontramos o volume específico ?

Através da tabela de saturação! Como o estado 2 é vapor d’água saturado , o volume específico é igual ao volume específico que está na linha da temperatura .
Passo 2
Já sabemos o título do estado 2. No entanto, como podemos descobrir o título do estado 1 para calcular a sua eneria interna específica ? Se liga na dica: se queremos encontrar o título da mistura saturada e já sabemos o seu volume específico, podemos usar a fórmula a seguir:
onde é o volume específico do vapor saturado na temperatura do estado 1 e é o volume específico do líquido saturado na temperatura do estado 1 .
Com esse valor, achamos a energia interna específica através da seguinte fórmula:
Agora só falta achar para calcular .
A massa da água pode ser encontrada reorganizando a equação de volume específico.
Como a massa da água não muda durante o aquecimento, esse valor que achamos para o estado 2 é igual ao valor de massa do estado 1.
Pronto, agora que temos todas as informações que precisamos, vamos iniciar nossos cálculos.
Passo 3
Começamos as contas, encontrando o valor de na tabela de saturação. Antes, precisamos lembrar que o estado 2 é vapor saturado de água.
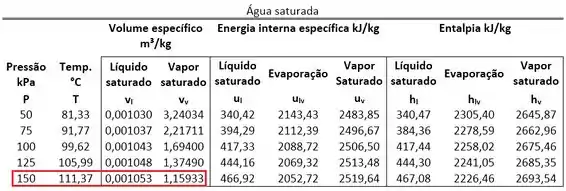
Como o volume específico do estado 1 é igual ao volume específico do estado 2:
Agora podemos encontrar o título da mistura saturada do estado 1, achando e através da mesma tabela de saturação.
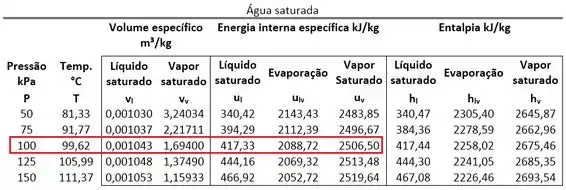
Com esse valor, podemos achar . Mas antes, temos que achar e . Esse será nosso próximo passo.
Passo 4
Na tabela de saturação, também encontramos os valores das energias internas de saturação que serão importantes para o cálculo de .
Substituindo esse valor na fórmula de :
Só falta calcular a massa de água para achar a energia interna .