Trabalho de Movimento da Fronteira
Produzido por Philip Canabarro BlockerTeoria
O tipo de trabalho mais comum em termodinâmica
Existe um tipo de trabalho para cada tipo de força: o trabalho elétrico é causado pela força elétrica, o trabalho de um eixo rotativo é causado por uma força aplicada fora do centro do eixo e o trabalho da gravidade é causado pelo campo gravitacional.
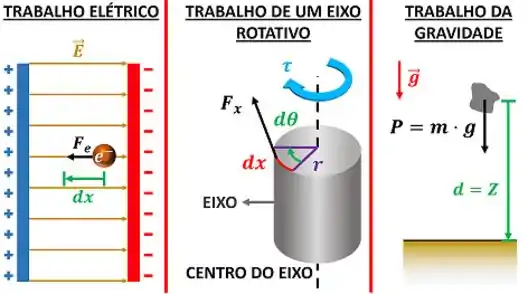
Conhecer os diferentes tipos de força e os tipos de movimento que cada força causa é fundamental para descobrir as fórmulas de cada classe de trabalho. Isso é importante, porque o cálculo do trabalho depende dessas duas variáveis.
O tipo de trabalho mais comum no estudo da eletricidade é o trabalho elétrico. O tipo de trabalho mais comum no estudo da queda livre é o trabalho da gravidade. Qual o trabalho mais comum em termodinâmica? O trabalho de movimento da fronteira de um sistema! Ele também pode ser chamado de trabalho de expansão do sistema.
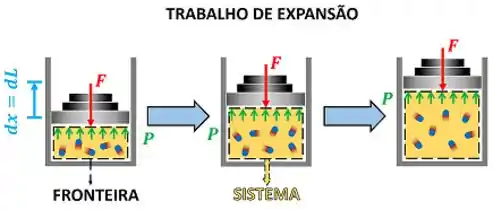
Fórmula do trabalho de expansão do sistema
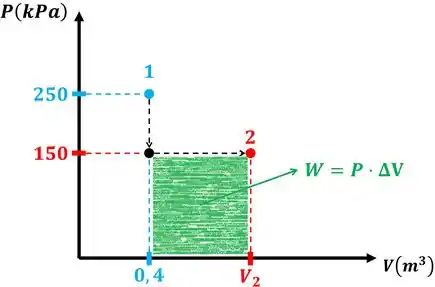
Como vimos na imagem acima, o trabalho de movimento da fronteira é causado pela pressão interna do sistema. Ou seja, o movimento da sua fronteira é causado pela força gerada por essa pressão. Logo:
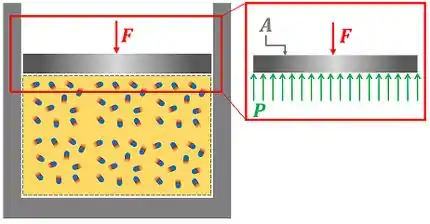
onde:
- é a pressão do sistema. Ela é medida em pascal de acordo com o Sistema Internacional de Unidades (S.I.);
- é a área do êmbolo que é perpendicular à força da pressão . Sua unidade é o metro quadrado no S.I.
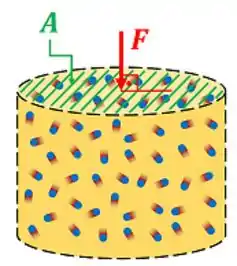
Só falta saber qual é o deslocamento da fronteira móvel, quando o pistão é empurrado para cima. Isso é visto na própria figura que apresenta o trabalho de expansão! Quando o conteúdo do cilindro-pistão pressiona o êmbolo, ele gera um deslocamento para cima.
Substituindo essas expressões de e a fórmula de trabalho fica:
Só que a área do pistão multiplicada pelo seu deslocamento é justamente o aumento do volume do sistema !
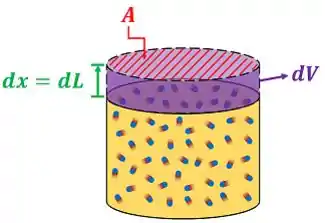
Por causa disso a fórmula final do trabalho de expansão do sistema vira:
Cálculo do trabalho através de um gráfico -
A integração de só pode ser realizada, se conhecemos o valor da pressão em função do volume durante o processo. Existem dois jeitos de conhecer essa relação entre pressão e volume do sistema: graficamente ou através de uma equação. Podemos entender a solução gráfica, vendo a curva formada por um processo de compressão do ar em um gráfico -.
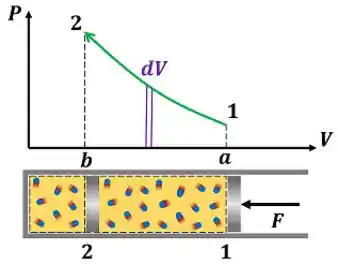
A curva do gráfico - representa o processo de compressão do ar dentro de um conjunto cilindro-pistão. Por ser um processo de compressão, o volume do estado inicial é maior do que o volume do estado final . Além disso, a pressão inicial é menor que a pressão final .
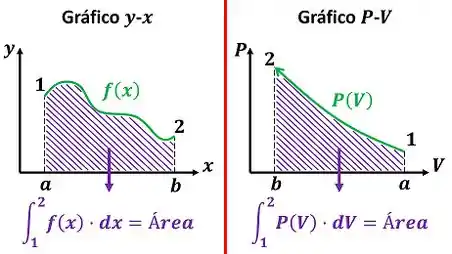
Vemos pela figura acima que, assim como a integral de uma função é igual à área abaixo da curva desenhada em um gráfico -, a integral da função é igual à área abaixo da curva traçado em um gráfico -. Agora vamos praticar o cálculo do trabalho graficamente!
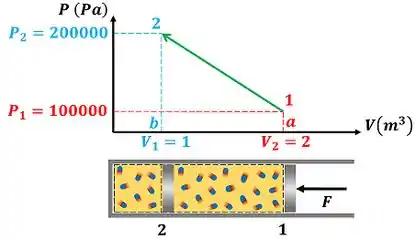
Vamos calcular o trabalho de compressão de um gás a partir do gráfico acima. Nele, vemos que a pressão varia linearmente entre seus estados inicial e final . Por causa disso, o valor de é igual à área do trapézio formado pelos pontos ---. Seu valor é negativo, porque foi um trabalho realizado sobre o sistema.
O trabalho realizado não é uma propriedade do sistema!
Vemos pelo gráfico -, que o processo linear de compressão é um dos vários caminhos que poderiam ligar os estados e . Ou seja, existem vários processos que poderiam levar o sistema do estado até o estado .
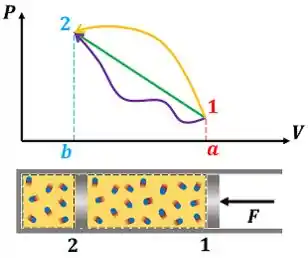
Como a área debaixo de cada curva é igual ao trabalho de cada processo, vemos que o valor do trabalho depende do trajeto que o sistema fez entre os estados e . Em outras palavras, precisamos saber qual o caminho que o sistema usou para chegar onde chegou. Isto é, precisamos saber a história do sistema para calcular o valor do trabalho que ele realizou !

A imagem acima relembra a pergunta que precisamos fazer para descobrir se uma variável é uma propriedade termodinâmica do sistema. Ela é uma propriedade, se conseguimos descobrir o seu valor sem precisar saber o processo que trouxe o sistema até o seu estado. Por causa disso, o trabalho realizado pelo sistema não pode ser considerado uma propriedade!
Trabalho realizado em um processo politrópico
Foi falado que existem dois jeitos de calcular o valor do trabalho. A forma gráfica já foi explicada. Resta entender como calcular o trabalho através de uma equação. O problema é que não existe apenas uma equação que represente todos os processos possíveis!

Calma! Não desista! Por mais que existam infinitas fórmulas para representar os infinitos caminhos, existe um tipo de processo que cai muito em provas de termodinâmica: o processo politrópico. Um processo politrópico é um processo com a fórmula igual a:
sendo:
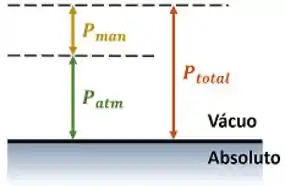
- é a pressão do sistema. Sua unidade é pascal de acordo com o S.I. Atenção! Apenas o valor de pressão absoluta deve ser substituído nessa equação. Não pode ser a pressão manométrica!
- um expoente que pode ter qualquer valor entre e . Para cada processo, tem um valor;
- é o valor do produto entre e . Para cada processo, essa constante tem um valor.
Ou seja, o valor da pressão de um processo politrópico sempre vale:
Agora, podemos substituir essa expressão na equação de trabalho de expansão para calcular a integral!
Existem duas soluções para essa integral: uma quando o expoente vale e outra quando o expoente é diferente de . Ao invés de encher sua cabeça com deduções desnecessárias de fórmulas, aqui estão as duas equações dos trabalhos de processos politrópicos prontinhas para você usar nas provas:
É importante lembrar que o índice é usado para indicar a pressão e o volume do estado inicial e o índice é usado para indicar a pressão e o volume do estado final .
Fórmula do trabalho de expansão do sistema
Cálculo do trabalho W através de um gráfico P - V
O trabalho realizado W não é uma propriedade do sistema!
Trabalho realizado em um processo politrópico P ⋅ V n = c o n s t a n t e
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Um gás contido em um cilindro-pistão expande isobaricamente, provocando uma variação de no seu volume. Considerando que este gás é mantido a no interior do cilindro, determine o trabalho realizado pelo gás em joule.
Passo 1
O exercício pede que a gente determine o trabalho de expansão de um gás. O gás faz uma força no êmbolo, colocando o ele em movimento. Esse movimento é possível, porque o gás está dando energia ao pistão através da força que ele produz. Chamamos essa forma de transferência de energia de trabalho.
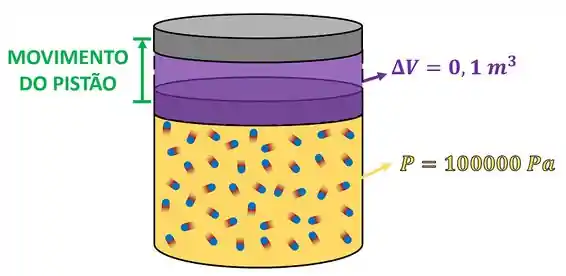
O nome desse tipo de trabalho de mudança de volume do sistema através do movimento de um pistão é chamado de trabalho de movimento da fronteira móvel do sistema. Isso quer dizer que podemos utilizar a seguinte fórmula para calcular o trabalho realizado pelo gás:
onde:
- é a pressão do gás em pascal . O enunciado fala que ela é igual a ;
- é o volume do gás em metro cúbico ;
- é o trabalho realizado pelo gás em joule . Essa é a incógnita do problema.
Mas como podemos usar essa integral. Por acaso sabemos o valor da pressão em função do volume apara conseguirmos fazer a integração? Sim! Sabemos! Foi dito que o gás se expande isobaricamente. Ou seja, a pressão do gás permanece constante durante o aumento de volume. Por isso, a fórmula do trabalho vira:
sendo a variação de volume do sistema durante o processo de expansão. Como o volume do gás aumenta, a variação do volume é positiva. Seu valor é dado pela questão.
Com esse valor, descobrimos que temos todas as informações que precisamos para calcular o trabalho. Então vamos para o próximos passo fazer isso!
Passo 2
Sabemos a pressão do gás e a sua variação de volume. Com isso, podemos achar o trabalho através da fórmula abaixo.
O gás realizou um trabalho de !
Resposta
Exercício Resolvido #2
Elaboração própria
de um gás perfeito a contido em um cilindro-pistão expande isobaricamente, provocando uma variação de no seu volume. Considerando que este gás ocupava antes da sua expansão, determine o trabalho realizado pelo gás em joule.
Passo 1
O exercício pede que a gente determine o trabalho de expansão de um gás. O gás faz uma força no êmbolo, colocando o ele em movimento. Esse movimento é possível, porque o gás está dando energia ao pistão através da força que ele produz. Chamamos essa forma de transferência de energia de trabalho.
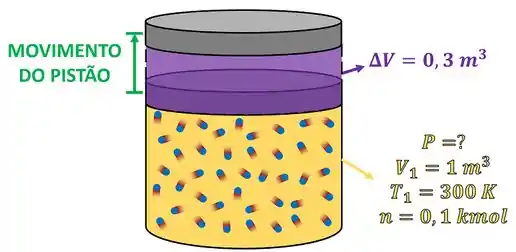
O nome desse tipo de trabalho de mudança de volume do sistema através do movimento de um pistão é chamado de trabalho de movimento da fronteira móvel do sistema. Isso quer dizer que podemos utilizar a seguinte fórmula para calcular o trabalho realizado pelo gás:
onde:
- é a pressão do gás em pascal ;
- é o volume do gás em metro cúbico ;
- é o trabalho realizado pelo gás em joule . Essa é a incógnita do problema.
Mas para usar essa fórmula, precisamos primeiro calcular a pressão inicial do gás. Para isso, usaremos a fórmula de gás perfeito.
sendo:
- ;
- é a constante universal dos gases. Seu valor é igual para todos os gases. Ela vale sempre ;
- é a temperatura do gás antes de expandir. Ela vale segundo o enunciado;
- é o volume que o gás ocupa antes de expandir. Ele vale segundo o enunciado.
Mas como podemos usar essa integral? Por acaso sabemos o valor da pressão em função do volume apara conseguirmos fazer a integração? Sim! Sabemos! Foi dito que o gás se expande isobaricamente. Ou seja, a pressão do gás permanece constante durante o aumento de volume. Logo:
Por isso, a fórmula do trabalho vira:
sendo a variação de volume do sistema durante o processo de expansão. Como o volume do gás aumenta, a variação do volume é positiva. Seu valor é dado pela questão.
Com esse valor, descobrimos que temos todas as informações que precisamos para calcular o trabalho. Então vamos para o próximos passo fazer isso!
Passo 2
Vamos iniciar os cálculos tentando encontrar pressão do gás.
Agora, sabemos a pressão do gás e a sua variação de volume. Com isso, podemos achar o trabalho através da fórmula abaixo.
O gás realizou um trabalho de !
Resposta
Exercício Resolvido #3
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 93-4.49
Um conjunto cilindro-pistão contém, inicialmente, de um gás a e . O gás é então expandido num processo onde . Admitindo que a pressão final seja igual a , determine o trabalho envolvido no processo.
Passo 1
O enunciado afirma que o processo que o gás passa mantém constante. Isso significa que a multiplicação entre a pressão inicial e o volume inicial é igual à multiplicação entre a pressão final e o volume final .
onde:
Esse é um processo politrópico. Processos politrópicos são processos durante os quais:
Como no nosso caso , esse é um processo politrópico com expoente igual a um.
Para esse processo politrópico com expoente igual a um, a fórmula do trabalho realizado entre os estados 1 e 2 é:
Só falta encontrar o valor de para calcular o trabalho. Ele é calculado reorganizando a fórmula do processo politrópico.
Pronto, temos todas as informações para calcular o trabalho. Vamos iniciar as contas no próximo passo!
Passo 2
Começamos as contas a partir de .
Com esse valor, conseguimos calcular .
Enfim, chegamos no resultado que a gente queria!
Resposta
Exercício Resolvido #4
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 93-4.50
Uma amostra de gás Hélio expande do estado inicial (, e ) até o estado final onde . Sabendo que a expansão é politrópica com , determine o trabalho realizado no processo.
Passo 1
O enunciado pede o trabalho realizado em um processo politrópico que vai do estado 1 (estado inicial) ao estado 2 (estado final) A fórmula de trabalho desse tipo de processo para expoentes diferentes de 1 é mostrada abaixo.
O problema nos diz o valor das seguintes variáveis:
Vemos, desta forma, que só falta achar o para terminar essa conta! Como podemos fazer isso então? Lembrando da seguinte fórmula de processo politrópico:
Reorganizando a fórmula, encontramos o volume final .
Depois de conhecer essa fórmula, estamos prontos para começar a calcular!
Passo 2
Começamos o cálculo a partir da determinação do volume final.
Colocando esse valor na fórmula de trabalho, chegamos no resultado que a gente queria!
Resposta
Exercício Resolvido #5
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 92-4.34
Um conjunto cilindro-pistão contém ar. Inicialmente, o ar está a , e o volume ocupado pelo ar é . Um processo a pressão constante é realizado e detecta-se o fornecimento de de trabalho. Determine o volume e a temperatura no estado final desse processo.
Passo 1
O enunciado diz que o ar do interior do cilindro recebe energia por trabalho. Esse trabalho é realizado a pressão constante. Por isso, podemos usar a fórmula simplificada de trabalho isobárico de movimento da fronteira.
O enunciado já informou o valor da pressão para a gente.
Além dele, o valor do trabalho também é informado. Foi falado que o gás realiza trabalho sobre a sua vizinhança. Pela regra dos sinais do trabalho, esse trabalho é positivo. O processo de variação do volume é uma expansão.
A variação do volume é dada pela fórmula:
onde:
- é o volume do gás depois da expansão. Ela é uma das incógnitas do problema;
- é o volume do gás antes da expansão. Ele vale segundo o enunciado.
Substituindo a fórmula de variação de volume na fórmula de trabalho, podemos achar uma equação para .
Já temos todas as informações para encontrar o volume final do gás. Falta entender como achar a temperatura final do gás. Vamos deixar isso para o próximo passo.
Passo 2
Achamos a temperatura final através da fórmula de gás perfeito.
onde é a constante universal dos gases. Seu valor é igual para todos os gases. Ela vale sempre . é o número de da substância presente no volume que ela ocupa. Descobrimos o seu valor, usando a fórmula de gás perfeito para o ar antes dele expandir.
Como o número de do ar não varia durante sua expansão, podemos usar o seu valor na fórmula de gás perfeito aplicada ao estado em que o ar se encontra depois da expansão.
Com isso conseguimos calcular tudo o que precisamos. Na próxima etapa iniciaremos as contas!
Passo 3
Inciamos os cálculos pela fórmula de volume final do gás.
Agora, vamos calcular o do gás.
Com esse valor, temos tudo o que precisamos para achar a temperatura final do gás.
Resposta
Exercício Resolvido #6
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 93-4.48
O conjunto cilindro-pistão mostrado na figura abaixo contém, inicialmente de dióxido de carbono a e . Os pesos são, então, adicionados a uma velocidade tal que o gás é comprimido segundo a relação . Admitindo que a temperatura final seja igual a , determine o trabalho realizado nesse processo.
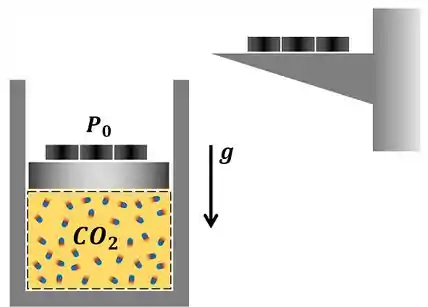
Passo 1
O exercício pede que a gente calcule o trabalho de um processo politrópico de compressão. Mas qual o expoente politrópico do processo? Podemos descobrir isso através da fórmula dada pelo próprio enunciado.
Pela fórmula vemos que o expoente vale 1,2.
A equação de trabalho de um processo politrópico para um expoente diferente de 1 é igual a:
onde o índice 1 aparece nas propriedades do estado 1 do dióxido de carbono e o índice 2 aparece nas propriedades do estado 2 do dióxido de carbono. O estado 1 é o estado inicial. Para ele temos as seguintes infomações.
Para o estado final sabemos apenas que:
Para descobrir a pressão e o volume desse estado, temos que usar a equação de gás perfeito para o estado 2.
Para saber o produto entre pressão e volume do estado 2 só falta encontrar o número de do dióxido de carbono. Como a massa de não varia durante esse processo politrópico, também não varia. Por causa disso, podemos encontrar o do estado 1 e usá-lo na equação do estado 2.
Pronto, temos tudo o que precisamos para calcular o trabalho. Vamos iniciar as contas no próximo passo!
Passo 2
Iniciamos os cálculos pelo valor de .
Agora conseguimos achar o produto entre pressão e volume finais.
Substituindo esse valor na fórmula de trabalho, encontramos:
Conseguimos!!! Achamos o trabalho realizado pelo dióxido de carbono.
Resposta
Exercício Resolvido #7
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 91-4.33
Um tanque de , (veja Figura), contém gás argônio a e . O cilindro , com um pistão que se movimenta sem atrito e massa tal que flutua com uma pressão interna de , está inicialmente vazio. A válvula que liga os dois recipientes é, então, aberta e o argônio escoa para e atinge um estado uniforme a e . Qual o trabalho realizado pelo argônio durante esse processo?
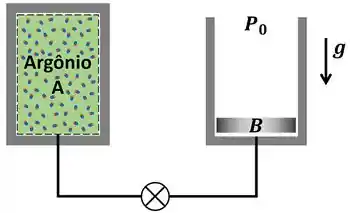
Passo 1
O exercício pede que a gente calcule o trabalho realizado pelo argônio, quando ele vai do estado 1 até o estado 2. O estado 1 é o estado do gás antes da abertura da válvula. O estado 2 é o estado do argônio depois do seu escoamento para ter terminado. A figura abaixo mostra todos os dados fornecidos pelo enunciado sobre os dois estados.
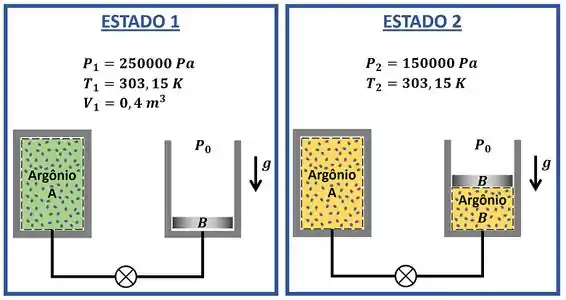
No entanto, o dado mais importante fornecido pelo enunciado está escondido nele! Ele está por trás da frase que fala sobre o pistão do cilindro : o pistão se movimenta sem atrito e tem massa tal que flutua com uma pressão interna de . Essa frase mostra que o pistão precisa de uma pressão de para se mover. Ou seja, quando a válvula é aberta, o argônio empurra a pistão com uma pressão de durante todo o processo. Mesmo que inicialmente a sua pressão seja maior . Mas por que isso acontece? Não era para a pressão diminuir aos poucos até alcançar ?

Você está correto em pensar assim! Na vida real, o processo seria dessa forma mesmo! Mas na termodinâmica nós usamos uma aproximação para todos os processos chamada de processo de quase-equilíbrio. Nesse processo, nós consideramos que todo o caminho percorrido pelo sistema é formado por estados de equilíbrio. Nesse estado. Não existe desequilíbrio! Portanto, a pressão interna do gás tem que estar equilibrada com a pressão causada pelo peso do pistão.
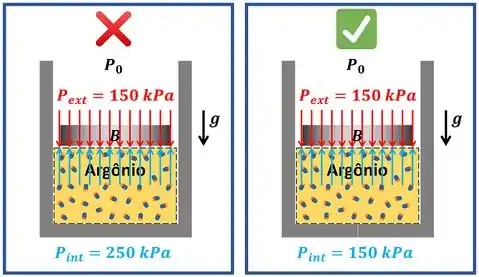
Resumindo, assim que a válvula abre, a pressão do argônio despenca de para . Segunda a nossa simplificação, ela muda instantaneamente e depois fica constante em .
Pelo gráfico de pressão versus volume, vemos que o trabalho relativo a essa mudança brusca de pressão é nula, porque a área embaixo dessa curva é nula. Mas também vemos que o trabalho que conta é de movimento de fronteira a pressão constante de .
Isso quer dizer que podemos usar a seguinte fórmula para calcular o trabalho.
onde é a pressão de e é a variação de volume de argônio dada pela equação:
precisa ser calculado através da fórmula de gás perfeito para o estado 2.
Como o processo não muda a massa de argônio, então ele também não muda o número de . Por isso, podemos calcular , aplicando a equação de gás perfeito para o estado 1.
Pronto, temos todas as informações que precisamos para iniciar os cálculos. Então vamos fazer isso na próxima etapa!
Passo 2
Começaremos as contas pela determinação de .
Agora conseguimos encontrar a volume final do argônio.
Enfim podemos usar a fórmula de trabalho!
Prontinho! Achamos o trabalho realizado pelo argônio!
Resposta
Exercício Resolvido #8
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 93-4.51
Uma amostra de ar é comprimida do estado inicial ( e ) até o estado final onde a temperatura é igual a e a pressão é igual a . Sabendo que a compressão é politrópica, determine o expoente relativo ao processo e o trabalho específico associado ao processo. Considere a massa molar do ar igual a .
Passo 1
O enunciado pede que a gente calcule o trabalho específico do processo politrópico. Mas o que é um trabalho específico? Assim como o volume específico é o volume dividido pela massa , o trabalho específico é o trabalho dividido pela massa.
O trabalho de um processo politrópico é igual a:
Então o trabalho específico desse processo é igual a:
O valor de foi dado pelo problema.
Já os valores de volumes específicos terão que ser calculados através das equações de gás perfeito. A fórmula de gás perfeito para o estado 1 é igual a:
é encontrado pela fórmula:
Achamos da mesma forma que achamos . Usamos a equação de gás perfeito para o estado 2.
Agora só falta acharmos o expoente politrópico . Mas isso ficará para o passo seguinte.
Passo 2
A primeira etapa para isso é olhar para a relação entre pressões e volumes desse processo.
Se dividirmos os dois lados pela massa elevada ao coeficiente politrópico , achamos que:
Reorganizando essa equação:
Como os dois lados da equação são iguais, os logaritmos dos dois lados da equação também serão iguais.
Usando as propriedades do logaritmo, chegamos a:
Com essa equação, temos tudo o que precisamos para iniciar nossos cálculos.
Passo 3
Começamos as contas por .
Depois disso, podemos calcular e .
Agora estamos aptos a achar o coeficiente politrópico.
Com esse valor, podemos usar a fórmula de trabalho específico.