Energia, Trabalho e Potência
Produzido por Philip Canabarro BlockerTeoria
O que é trabalho?
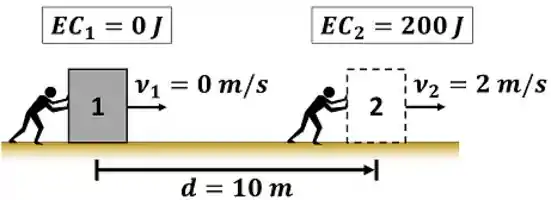
Imagine um bloco de metal parado com massa de . Nesse momento, sua energia cinética é nula, porque a velocidade do bloco vale .
Agora imagine que uma academia criou um novo exercício infalível para ficar musculoso: os alunos precisam empurrar esse bloco com uma força até ele atingir uma velocidade de após percorrer uma distância de .

Se os clientes cumprirem essa tarefa, quanto valerá a energia cinética do bloco no fim da atividade?
Ou seja, a energia do bloco aumentou! Mas se a energia se conserva, de onde ela veio? A energia passou dos alunos para o bloco a partir da força que eles fizeram para empurrá-lo, enquanto percorriam uma distância . Chamamos essa forma de transferência de energia, que acontece por causa de uma força, de trabalho.
Como se calcula a energia transferida por trabalho ?
Se não existe atrito nem outras forças atuando sobre o bloco de metal, a força feita pelos alunos será a única fonte de energia do bloco. Sem a dissipação, toda a energia doada por eles será convertida em energia cinética. Nessa situação especial, conseguimos medir a quantidade de energia transferida por trabalho através da diferença entre a energia final e inicial do bloco.
onde:
- é a quantidade de energia transferida por trabalho dos alunos. Para simplificar, chamamos essa quantidade de energia transferida de trabalho. Essa variável é medida em joule de acordo com o Sistema Internacional (S.I.);
- é a energia cinética do bloco depois de ser empurrado, medida em conforme o S.I.;
- é a energia cinética do bloco parado, medida em conforme o S.I.
Em alguns exercícios de termodinâmica a energia transferida por trabalho não é convertida apenas em energia cinética. Ela pode ser convertida em energia potencial ou dissipada em calor, por exemplo. Ou seja, as vezes as situações são mais complexas e não saberemos as energias final e inicial do objeto movimentado. Nesses casos, como podemos calcular ?
sendo:
- a força aplicada sobre o objeto na direção do seu deslocamento em newton ;
- o estado do objeto antes da ação da força e o estado do objeto depois da ação da força;
- o deslocamento infinitesimal do objeto.
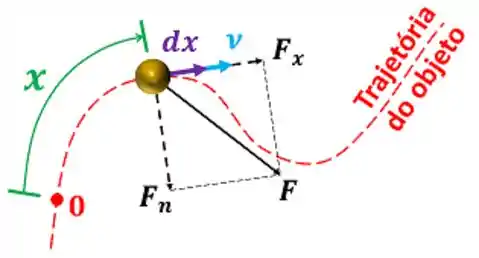
Em outras palavras, podemos calcular o trabalho, se conhecemos como força varia ao longo da trajetória. Por exemplo: se os alunos da academia empurram o bloco de metal com uma força constante de no mesmo sentido do deslocamento do bloco, o trabalho realizado pela força deles vale:
Esse valor obtido é igual ao valor calculado do jeito anterior!
O que significa um valor de trabalho negativo?
O trabalho realizado pelos alunos equivale a . Ou seja, os alunos transferiram de energia do próprio corpo para o bloco. Esse valor de trabalho realizado pelos clientes é positivo. Porém, em alguns problemas de termodinâmica o aparecerá com um valor negativo. O que poderia significar uma transferência de energia menor que zero?

Vamos entender isso com o exemplo de um gás dentro de um conjunto cilindro-pistão. Quando o gás empurra o êmbolo pra cima, através da força causada pela sua pressão interna, ele realiza trabalho sobre a sua vizinhança.
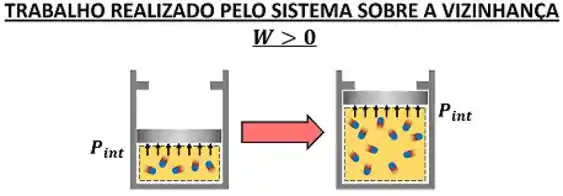
Nesse caso, o sistema composto pela massa de gás está cedendo energia para o ambiente ao redor. Quando isso ocorre, temos que:
Ou seja, o trabalho positivo é o trabalho realizado pelo sistema sobre sua vizinhança.
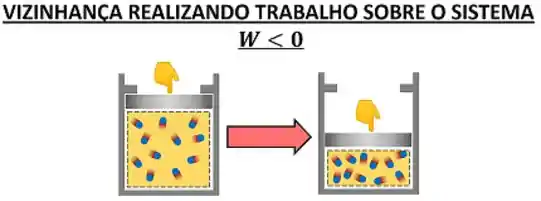
Quando uma pressão externa empurra o êmbolo para baixo, dizemos que o trabalho é realizado sobre o sistema. Nesse caso, o sistema está recebendo energia do ambiente ao redor. Nesse cenário, consideramos que:
Corrente elétrica atravessando a fronteira é trabalho?
O trabalho foi definido como um tipo de transferência de energia causada por uma força. No entanto, as vezes podemos ficar em dúvida para saber se uma transferência de energia é ocasionada por uma força ou não. Esse é o caso de um motor, sendo alimentado por uma bateria. Essa transferência de energia elétrica entre os dois pode ser chamada de trabalho?
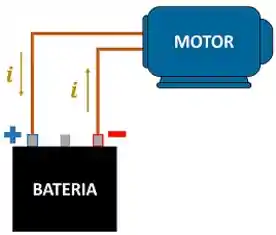
Podemos refazer a pergunta, usando a definição de trabalho e de sistema: a transferência de energia elétrica que atravessa a fronteira do motor é causada por uma força? Sim! Se ampliarmos bastante a visão que temos do condutor elétrico, veremos que os elétrons se movimentam por conta da força elétrica!
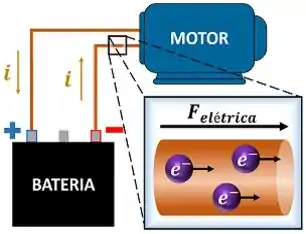
Ou seja, o fluxo de elétrons atravessando uma fronteira sempre pode ser chamado de trabalho. Mas ainda fica um questionamento. Se considerarmos o motor como o nosso sistema, a energia elétrica recebida por ele é um trabalho positivo ou negativo?
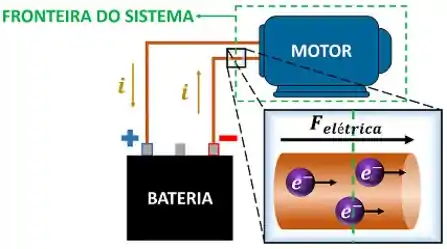
Como o motor está recebendo energia da vizinhança, falamos que o ambiente está realizando trabalho sobre o motor. Logo, para esse caso:
Potência
Se um carro consegue subir rápido uma ladeira muito inclinada, dizemos que o seu motor é potente. Ou seja, se o motor do carro consegue gerar uma grande força capaz de empurrar rápido todo o peso do veículo, nós dizemos que ele é potente.
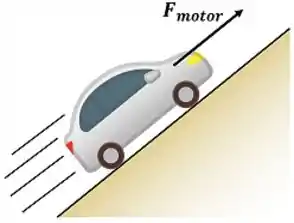
Na termodinâmica, medimos a potência da mesma forma: quanto mais rápido um aluno da academia empurra o bloco de metal, maior a potência da sua força. Isto é, a potência mede a velocidade e intensidade do trabalho. A fórmula da potência se encontra abaixo.
onde:
- é a derivada do trabalho em função do tempo. Sua unidade no S.I. é joule por segundo ou watt . Essas duas unidades são equivalentes:
- também é a derivada do trabalho em função do tempo. Só que escrita de outra forma.
Assim como calculamos a velocidade do deslocamento derivando ele em relação ao tempo, calculamos essa velocidade de realização do trabalho, derivando trabalho em relação ao tempo. No decorrer das teorias de termodinâmica, sempre usaremos esse pontinho em cima de uma variável para representar sua derivação no tempo.
Usando a fórmula de trabalho em função da força , temos:
é a velocidade do objeto empurrado pela força . Ela é medida em metro por segundo segundo o S.I.
Potência de um eixo girando
Calculamos a potência de uma força que causa um movimento de translação. Mas e se a força causar um movimento de rotação, como poderíamos calcular sua potência?
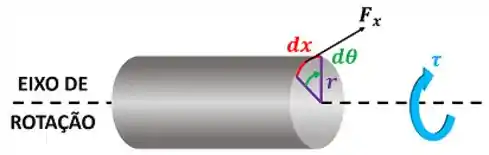
Nesse caso, consideramos que a força gera um torque :
é o raio da seção transversal do eixo, medido em metro de acordo com o S.I. O torque é medido em newton-metro .
Além disso, o eixo gira a uma velocidade angular com equação igual a:
Com essas fórmulas, deduzimos a seguinte expressão para a potência do giro:
Agora vamos resolver os exercícios para treinar os conceitos dados nessa teoria.
O que significa um valor de trabalho W negativo?
Corrente elétrica atravessando a fronteira é trabalho?
Potência W ˙
Potência de um eixo girando
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
O eixo de um ventilador gira com a velocidade igual a . O motor elétrico impõe um torque de . Calcule a potência de giro desse eixo.
Passo 1
O motor tem que aplicar uma força ao eixo para fazer ele girar. Ou seja, o motor deve dar energia ao eixo através dessa força. Por causa disso, dizemos que o motor realiza trabalho no eixo.
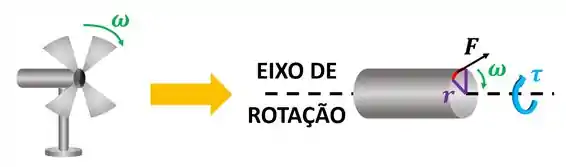
A taxa de energia que esse motor entrega ao eixo por unidade de tempo é chamada de potência. A fórmula de potência para o eixo girando é dada por:
onde:
- é a potência de giro do eixo. Ela é a incógnita do problema. Sua unidade no Sistema Internacional (S.I.) é o watt ;
- é o torque aplicado ao eixo. Sua unidade em S.I. é o newton-metro . Ele é dado pelo enunciado.
- é a velocidade angular de giro do eixo. Sua unidade é o radiano por segundo . Seu valor foi informado pela questão.
Então, para achar a potência precisamos substituir os dados na equação. Vamos deixar isso pro próximo passo.
Passo 2
Substituindo os valores na fórmula, temos:
Achamos o resultado final!
Resposta
Exercício Resolvido #2
Elaboração própria
Duas engrenagens estão girando acopladas. A engrenagem motora empurra a engrenagem movida com uma força de . O ponto de contato entre elas está a de distância do centro da engrenagem motora. A engrenagem motora gira com velocidade de . Qual a potência de giro da engrenagem motora?
Passo 1
Nesse exercício, a engrenagem motora passa energia para a engrenagem movida por meio de trabalho.
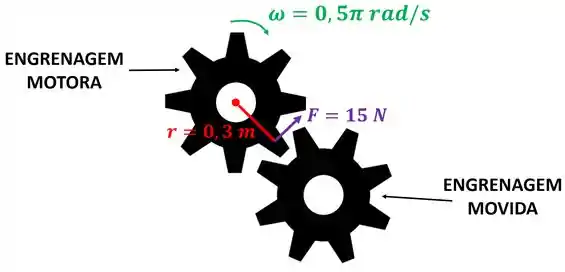
A taxa de energia transmitida por unidade de tempo é a potência de giro da engrenagem motora . Essa é a incógnita do problema. Para calcular, usamos a fórmula de potência de rotação.
onde:
- é a potência de giro do eixo. Ela é a incógnita do problema. Sua unidade no Sistema Internacional (S.I.) é o watt ;
- é o torque aplicado ao eixo. Sua unidade em S.I. é o newton-metro . Ele é dado pelo enunciado indiretamente através da força e do raio de aplicação dela.
- é a velocidade angular de giro do eixo. Sua unidade é o radiano por segundo . Seu valor foi informado pela questão.
Então, para achar a potência precisamos substituir os dados na equação. Vamos deixar isso pro próximo passo.
Passo 2
Substituindo os valores na fórmula, temos:
Achamos o resultado final!
Resposta
Exercício Resolvido #3
Elaboração própria
Considere um sistema composto por um gás perfeito no interior de um conjunto cilindro-pistão. Uma força de tenta pressionar o pistão para baixo. A pressão do gás é igual a . O pistão possui um diâmetro de . O sistema realiza trabalho sobre a vizinhança ou a vizinhança realiza trabalho sobre o pistão? O trabalho é positivo ou negativo?
Passo 1
O enunciado pede para que a gente determine se o trabalho é realizado pelo sistema ou se ele é realizado sobre o sistema. Como podemos descobrir isso? Observando a variação de volume do sistema. Se o volume aumenta, o pistão sobe e o sistema realiza trabalho sobre a vizinhança. Quando isso acontece, o trabalho é positivo!
Se o volume diminui, o pistão desce e a vizinhança realiza trabalho sobre o sistema. Quando isso acontece, o trabalho é negativo!
Isso é só uma convenção de sinais! Ou seja, determinamos o que consideramos como trabalho positivo ou negativo antes para facilitar nossos cálculos mais tarde!
Ou seja, agora o objetivo do exercício mudou! Antes era pra descobrir o sinal do trabalho. Agora é pra saber se o volume do sistema aumenta ou diminui.
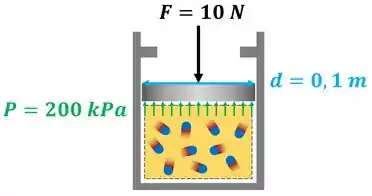
Mas como podemos saber se o volume do sistema aumenta ou diminui? Descobrindo para onde o pistão se move. Se a força para baixo for maior que a força da pressão interna do gás pra cima , o pistão desce e o volume diminui. Se a força da pressão do gás pra cima for maior que a força pra baixo, o pistão sobe.
A força é dada pelo enunciado.
E como podemos calcular a força que o gás aplica no pistão ? Reorganizando a fórmula da pressão.
é dado pelo problema.
Fica faltando a área do pistão para conseguir calcular . Isso é informado indiretamente através do valor do diâmetro do pistão .
Agora vamos substituir os valores que temos nessas fórmulas para descobrir o sinal do trabalho! Mas isso vai ficar pra próxima etapa!
Passo 2
Primeiro precisamos calcular a área do pistão.
Com esse valor, descobrimos a força do gás .
Agora vamos comparar essa força com a força para descobrir se o pistão sobe ou desce.
O pistão sobe! Logo, o volume do sistema aumenta. Por causa disso, o sistema realiza trabalho sobre o ambiente. Por isso:
Resposta
O sistema realiza trabalho sobre a vizinhança. O trabalho é positivo.
Exercício Resolvido #4
Elaboração própria
A figura abaixo mostra um motor elétrico acionado por uma bateria. Esse motor faz um eixo girar. Como consequência, a hélice acoplada ao eixo também gira e agita o gás presente em um tanque rígido.
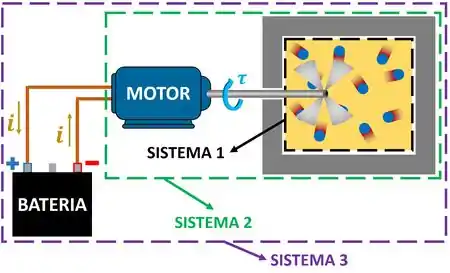
Considere três sistemas. Cada um formado por uma fronteira diferente. O sistema 1 é representado pelo gás no interior do tanque. O sistema 2 inclui o tanque e o motor elétrico. O sistema 3 inclui o tanque, o motor elétrico e a bateria. Determine se esses três sistemas realizam trabalho sobre a vizinhança ou se a vizinhança realiza trabalho sobre eles. Para cada sistema, diga se o trabalho é positivo ou negativo.
Passo 1
O exercício pede que a gente saiba se os sistemas estão recebendo energia ou se estão dando energia. Se eles estão dando energia, eles estão realizando trabalho sobre a vizinhança. Nesse caso, o trabalho é considerado positivo.
Se eles estão recebendo energia, a vizinhança está realizando trabalho sobre eles. Nesse caso, o trabalho é negativo.
Então vamos analisar caso a caso se esses três sistemas realizam ou recebem trabalho.
O primeiro passo é entender o motivo dessas transferências de energia serem consideradas trabalho. Vamos falar sobre cada um dos sistemas em passos separados.
Passo 2
O sistema 1 é formado pelo gás do interior do tanque. Esse gás é agitado por uma hélice girando. Isso pode confundir, porque o que atravessa a fronteira do sistema 1 não é uma força , mas sim um torque . Ou seja, podemos ficar em dúvida se a transferência de energia é ou não é trabalho.
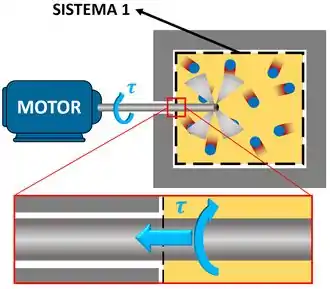
Para acabar com essa dúvida, prcisamos lembrar que onde tem torque, tem força. O torque em um eixo é sempre causado por uma força que não passa pelo eixo.
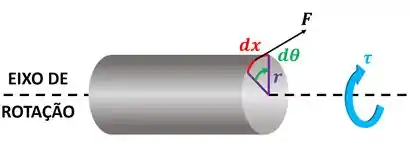
Ok! Agora sabemos que a troca de energia acontece por causa do trabalho. Mas a energia stá saindo do sistema 1 ou entrando no sistema 1? Para entender isso, temos que perguntar: qual é o efeito do movimento da hélice sobre as moléculas de gás? Ela agita eles! O choque entre a hélice e as moléculas faz as moléculas ganharem energia cinética! Então a energia entra!
Como o sistema 1 recebe energia, o trabalho do sistema 1 é negativo! A vizinhança realiza trabalho sobre o sistema 1.
Passo 3
Apenas os fios elétricos que alimentam o motor atravessam a fronteira do sistema 2.
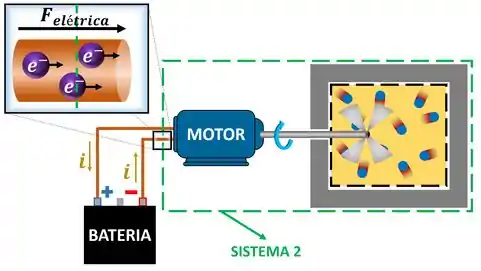
Por causa disso, pode ficar difícil de entender se a troca de energia entre o sistema 2 e a sua vizinhança é considerada trabalho ou não. Mas isso se resolve se a gente lembrar que para os elétrons se movimentarem eles precisam de a força elétrica. Por isso a troca de energia elétrica é considerada trabalho. Como os elétrons estão entrando no sistema 2, eles estão carregando para dentro desse sistema sua própria energia.
Então o sistema 2 recebe energia da sua vizinhança. Em outras palavras, a vizinhança realiza trabalho sobre o sistema 2. Por conta disso o trabalho desse sistema é negativo!
Passo 4
Se a gente observar o sistema 3, veremos eu nada entra ou sai da sua fronteira. Todas as trocas de energia são dentro do sistema 3. Ou seja, não existe troca de energia entre o sistema 3 e a sua vizinhança. Por causa disso, dizemos que o trabalho do sistema 3 é zero. Ele não realiza trabalho sobre a vizinhança nem sofre trabalho da vizinhança.
Resposta
Exercício Resolvido #5
Elaboração própria
Considere um sistema composto por um gás perfeito no interior de um conjunto cilindro-pistão. O êmbolo está inicialmente travado por pinos e sobre ele é posto um peso de . A pressão do gás é igual a . Após a remoção dos pinos, o pistão se movimenta. O sistema realiza trabalho sobre a vizinhança ou a vizinhança realiza trabalho sobre o sistema? O trabalho é positivo ou negativo? Considere que o pistão possua um diâmetro de e que a pressão atmosférica sobre o êmbolo valha . Além disso, suponha que a massa do pistão seja desprezível.
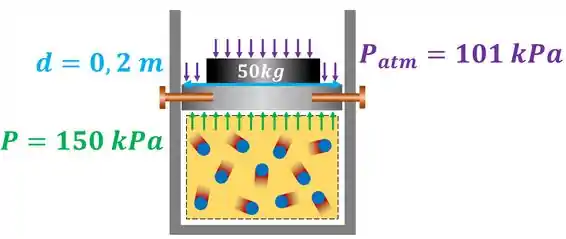
Passo 1
O enunciado pede para que a gente determine se o trabalho é realizado pelo sistema ou se ele é realizado sobre o sistema. Como podemos descobrir isso? Observando a variação de volume do sistema depois que os pinos são removidos! Se o volume aumenta, o pistão sobe e o sistema realiza trabalho sobre a vizinhança. Quando isso acontece, o trabalho é positivo!
Se o volume diminui, o pistão desce e a vizinhança realiza trabalho sobre o sistema. Quando isso acontece, o trabalho é negativo!
Ou seja, agora o objetivo do exercício mudou! Antes era pra descobrir o sinal do trabalho. Agora é pra saber se o volume do sistema aumenta ou diminui.
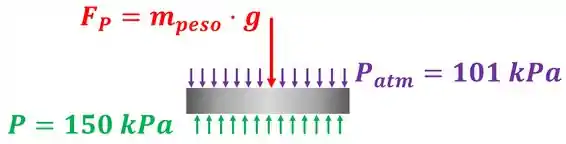
Mas como podemos saber se o volume do sistema aumenta ou diminui? Descobrindo para onde o pistão se move. Se a força do peso e a força da pressão atmosférica juntas forem maior que a força da pressão interna do gás , o pistão desce e o volume diminui. Caso contrário, o pistão sobe.
No próximo passo vamos aprender a calcular essas forças!
Passo 2
A força é dada indiretamente pelo enunciado, por meio da massa do peso.
A força da pressão que o ar aplica sobre o êmbolo é calculada através da fórmula da pressão.
é informada é vale:
A área do pistão é informada indiretamente através do valor do diâmetro do pistão .
E como podemos calcular a força que o gás aplica no pistão ? Reorganizando a fórmula da pressão.
é dado pelo problema.
Agora vamos substituir os valores que temos nessas fórmulas para descobrir o sinal do trabalho! Mas isso vai ficar pra próxima etapa!
Passo 3
Primeiro precisamos calcular a área do pistão.
Com esse valor, descobrimos a força do gás .
Sabendo a área do pistão também somos capas de encontrar .
A soma entre as duas forças ( e ) que tentam empurrar o pistão pra baixo vale:
Agora vamos comparar essa soma de forças com a força para descobrir se o pistão sobe ou desce.
O pistão sobe! Logo, o volume do sistema aumenta. Por causa disso, o sistema realiza trabalho sobre o ambiente. Por isso:
Resposta
O sistema realiza trabalho sobre a vizinhança. O trabalho é positivo.
Exercício Resolvido #6
Elaboração própria
Considere um sistema composto por gás perfeito no interior de um conjunto cilindro-pistão. O êmbolo está inicialmente travado por pinos e sobre ele é posto um peso de . Nesse instante o gás ocupa do cilindro e se encontra a . Após a remoção dos pinos, o pistão se movimenta. O sistema realiza trabalho sobre a vizinhança ou a vizinhança realiza trabalho sobre o sistema? O trabalho é positivo ou negativo? Considere que o pistão possua um diâmetro de e que a pressão atmosférica sobre o êmbolo valha . Além disso, suponha que a massa do pistão seja desprezível.
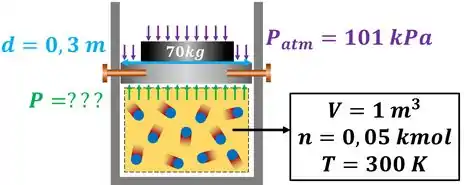
Passo 1
O enunciado pede para que a gente determine se o trabalho é realizado pelo sistema ou se ele é realizado sobre o sistema. Como podemos descobrir isso? Observando a variação de volume do sistema depois que os pinos são removidos! Se o volume aumenta, o pistão sobe e o sistema realiza trabalho sobre a vizinhança. Quando isso acontece, o trabalho é positivo!
Se o volume diminui, o pistão desce e a vizinhança realiza trabalho sobre o sistema. Quando isso acontece, o trabalho é negativo!
Ou seja, agora o objetivo do exercício mudou! Antes era pra descobrir o sinal do trabalho. Agora é pra saber se o volume do sistema aumenta ou diminui.
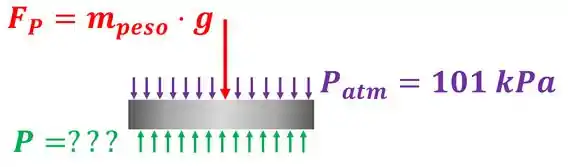
Mas como podemos saber se o volume do sistema aumenta ou diminui? Descobrindo para onde o pistão se move. Se a força do peso e a força da pressão atmosférica juntas forem maior que a força da pressão interna do gás , o pistão desce e o volume diminui. Caso contrário, o pistão sobe.
No próximo passo vamos aprender a calcular essas forças!
Passo 2
A força é dada indiretamente pelo enunciado, por meio da massa do peso.
A força da pressão que o ar aplica sobre o êmbolo é calculada através da fórmula da pressão.
é informada é vale:
A área do pistão é informada indiretamente através do valor do diâmetro do pistão .
E como podemos calcular a força que o gás aplica no pistão ? Reorganizando a fórmula da pressão.
é dado indiretamente pelo problema. Para calculá-lo, precisamos reorganizar a fórmula de gás perfeito.
Agora vamos substituir os valores que temos nessas fórmulas para descobrir o sinal do trabalho! Mas isso vai ficar pra próxima etapa!
Passo 3
Primeiro precisamos calcular a área do pistão.
Sabendo a área do pistão também somos capas de encontrar .
Agora precisamos calcular a pressão do gás perfeito.
Com esse valor, descobrimos a força do gás .
A soma entre as duas forças ( e ) que tentam empurrar o pistão pra baixo vale:
Agora vamos comparar essa soma de forças com a força para descobrir se o pistão sobe ou desce.
O pistão sobe! Logo, o volume do sistema aumenta. Por causa disso, o sistema realiza trabalho sobre a vizinhança. Por isso:
Resposta
O sistema realiza trabalho sobre a vizinhança. O trabalho é positivo.
Exercício Resolvido #7
Elaboração própria
Um tanque rígido de contém de e de ar separados por um pistão móvel. O êmbolo está inicialmente travado por pinos. Nesta condição, o ocupa do tanque. Considere que ambos os gases perfeitos possuem a mesma temperatura. Além disso, suponha que a massa molar do vale e que a massa molar do ar vale . Após a remoção dos pinos, o pistão se movimenta. Quando isso ocorre, o realiza trabalho sobre o ar ou o ar realiza trabalho sobre o ?
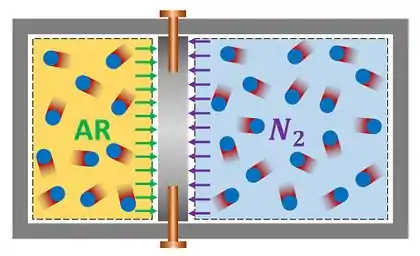
Passo 1
O enunciado pede para que a gente determine se o trabalho é realizado pelo ar ou se ele é realizado pelo . Antes de resolver isso, vamos listar os dados fornecidos pelo enunciado e as incógnitas do problema com uma figura para organizar os pensamentos.
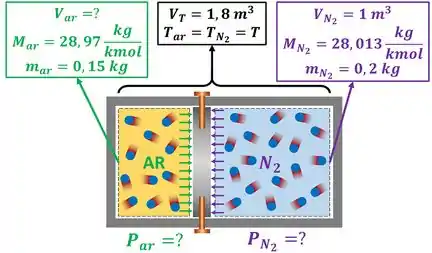
Como podemos descobrir quem realiza trabalho em quem? Observando a variação de volume dos gases depois que os pinos são removidos! Se o volume ocupado pelo ar aumenta, o pistão é deslocado pra direita e o ar realiza trabalho sobre o .
onde é o trabalho realizado pelo gás nitrogênio .
Se o volume ocupado pelo ar diminui, o pistão se desloca pra esquerda e o realiza trabalho sobre o ar.
Ou seja, agora o objetivo do exercício mudou! Antes era pra descobrir o sinal do trabalho. Agora é pra saber se os volumes dos gases aumentam ou diminuem. Já é um avanço!

Mas como podemos saber se o volume do sistema aumenta ou diminui? Descobrindo para onde o pistão se move. Se a pressão do ar antes do pino ser removido for maior que a pressão do nitrogênio , o pistão vai pra direita e o volume do ar aumenta. Caso contrário, o pistão vai pra esquerda e o volume do ar diminui.

No próximo passo vamos aprender a calcular essas pressões!
Passo 2
As pressões dos gases são dadas indiretamente pelo problema. Para calculá-las, precisamos reorganizar a fórmula de gás perfeito. Para o ar, temos que:
O volume do ar também é dado indiretamente por meio do volume total do tanque e do volume ocupado pelo
Já é encontrado pela fórmula:
A pressão do nitrogênio é obtida da mesma forma.
O é encontrado pela fórmula:
Agora vamos substituir os valores que temos nessas fórmulas para descobrir o que queremos! Mas isso vai ficar pra próxima etapa!
Passo 3
A primeira etapa é calcular .
Sabendo disso, pulamos para o cálculo do volume ocupado pelo ar, antes das travas do pistão serem removidas.
Com esses resultados, substituímos os valores na fórmula de pressão do ar.
Agora é a vez de iniciarmos os cálculos da pressão do . Começamos os cálculos pelo .
Com esse valor, podemos encontrar a pressão do nitrogênio em função da sua temperatura.
Comparando as duas pressões, vemos que:
Isso quer dizer que o pistão vai se mover pra esquerda e o volume de ar vai diminuir. Ou seja, o realiza trabalho no ar!
Resposta
O realiza trabalho no ar.
Exercício Resolvido #8
Elaboração própria
Um tanque rígido de contém de , de ar e de hélio separados por dois pistões móveis. Os êmbolos estão inicialmente travados por pinos. Nesta condição, o ocupa do tanque e o ocupa . Considere que os três gases perfeitos possuem de temperatura. Além disso, suponha que a massa molar do vale , que a massa molar do ar vale e que a massa molar do vale . Após a remoção dos pinos, os pistões se movimentam. As temperaturas de todos os gases permanecem constantes durante toda a movimentação. Após os pistões pararem, determine se cada gás realizou ou sofreu trabalho durante o reposicionamento dos êmbolos.
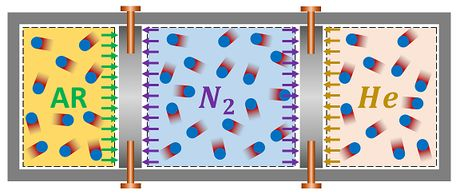
Passo 1
O enunciado pede para que a gente determine se o trabalho é realizado por cada gás ou se ele é realizado sobre cada gás. Mas antes de resolver isso, vamos listar os dados fornecidos pelo enunciado com uma figura para organizar os pensamentos.
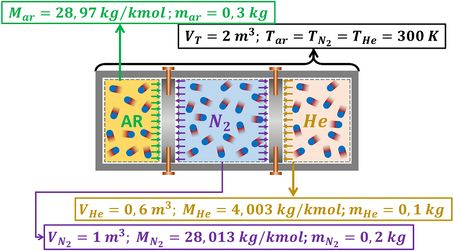
Como podemos descobrir se o gás realiza ou sofre trabalho? Observando a variação de volume dos gases depois que os pinos são removidos! Por exemplo, se o volume ocupado pelo ar aumenta, o ar realiza trabalho . Se ele diminui, o ar sofre trabalho.
onde é o volume do ar antes de removerem os pinos e é o volume ocupado pelo ar depois de removerem os pinos.
Essa regra de variação de volume serve para os outros dois gases também!
Os volumes e foram dados pelo enunciado.
O volume foi fornecido de forma indireta pelo enunciado, quando ele disse o volume total do tanque rígido .
Mas como podemos determinar os volumes de cada gás depois do pino ser removido e os pistões se equilibrarem em uma nova posição?
Dividimos essa tarefa em três etapas:
- Achar as pressões dos gases antes das travas dos pistões serem removidas através das fórmulas de gás perfeito;
- Achar as pressões dos gases depois das travas dos pistões serem removidas através das fórmulas de gás perfeito, lembrando que as temperaturas dos gases não variam;
- Achar os volumes ocupados pelos gases depois da remoção das travas .
Ufa! Quanta coisa! É muita coisa mesmo! Mas resolver o problema em etapas vai facilitar o entendimento.
No próximo passo vamos descobrir como calcular as pressões iniciais de cada gás!
Passo 2
As pressões dos gases, de quando os pinos ainda não tinham sido removidos, são dadas indiretamente pelo problema. Para calculá-las, precisamos reorganizar a fórmula de gás perfeito. Para o ar, temos que:
é encontrado pela fórmula:
A pressão do nitrogênio é obtida da mesma forma.
O é encontrado pela fórmula:
Por fim, a pressão do hélio é encontrada pela mesma equação.
O é encontrado pela fórmula:
Agora que já sabemos calcular as pressões iniciais, vamos calcular as pressões finais .
Passo 3
Existem três informações escondidas no enunciado. Elas são fundamentais para o cálculo das pressões finais! A primeira é que essas pressões finais são todas iguais.
Essa informação está implícita na questão, quando o enunciado diz que os pistões param. Se eles param quer dizer que todas as pressões se equilibrar e fazem a mesma força nos êmbolos.
Também precisamos lembrar que as massas, assim como as temperaturas, permanecem iguais durante o movimento dos pistões.
Por último, devemos lembrar que o volume do tanque rígido não varia. Ou seja, a soma de todos os volumes finais ocupados pelos gases continua sendo igual a .
Com essas informações, somos capazes de desenvolver as fórmulas das pressões finais. A primeira etapa é usar a informação de que as temperaturas permanecem constantes durante o movimento dos pistões. Se isso é verdade, temos que:
Se esses valores são constantes, os valores finais e iniciais são iguais.
Reorganizando essas equações, já encontramos uma fórmula para .
No entanto, ainda não conhecemos as pressões finais. Só sabemos que elas são iguais. De qualquer forma, podemos usar essa igualdade para achar uma nova expressão para os volumes finais.
Usando essas fórmulas na equação da soma dos volumes, achamos que:
Reorganizando a equação, descobrimos que:
Pronto, achamos as pressões finais! Além disso, podemos usar esse valor de para encontrar os volumes finais nas fórmulas acima!
Então vamos começar a fazer os cálculos pra chegar nos volumes finais!
Passo 4
A primeira etapa é calcular , e .
Sabendo disso, pulamos para o cálculo do volume ocupado pelo ar, antes das travas do pistão serem removidas.
Com esses resultados, substituímos os valores nas fórmulas de pressão inicial.
Com as pressões iniciais, descobrimos a pressão final de todos os gases.
Por fim, conseguimos achar os volumes finais, substituindo as pressões finais nas fórmulas.
Com esses valores, decobrimos que: o volume do ar aumentou, o volume do hélio aumentou e o volume do diminuiu. Isso significa que o ar realizou trabalho, o hélio realizou trabalho e o nitrogênio sofreu trabalho!
Resposta
O ar realizou trabalho, o hélio realizou trabalho e o nitrogênio sofreu trabalho!