Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 75
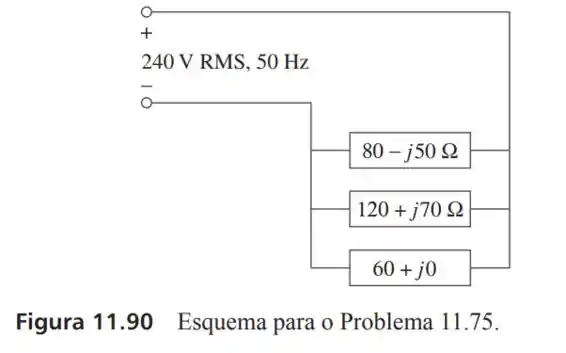
75- Considere o sistema de potência mostrado na Figura . Calcule :
A potência complexa total
O fator de potência
Passo 1
O macete aqui é calcular a potência total em todas as impedâncias, já que todas elas estão sendo colocadas sobre a mesma tensão. E a fórmula é a seguinte:
Pela impedância de nós temos a seguinte potência:
Já a a potência na impedância de será:
Já a potência na impedância de ou simplesmente a resistência de .
Então a potência complexa total será:
Passo 2
E o fator de potência será:
E como a potência reativa é negativa então a reatância da impedância total é capacitiva. Tendo um fator de potência adiantado.
Resposta
Exercícios de Livros Relacionados
As duas cargas mostradas na Figura P10.22 podem ser descritas da seguinte forma: a carga 1 absorve uma potência média de 10 kW e uma potência reativa de 4 kVAR; a carga 2 tem uma impedância de (60 + j
Suponha que o circuito da Figura P10.24 represente um circuito de distribuição residencial no qual as impedâncias dos condutores são desprezíveis e Vg1 = Vg2 = 110/0° V (ef). As três cargas no circuit
a) Determine VL (ef) e θ para o circuito da Figura P10.19, se a carga absorver 2.500 VA, com um fator de potência atrasado de 0,8. b) Construa um diagrama fasorial de cada solução obtida em (a).
Os valores dos parâmetros do circuito da Figura P10.56 são L 1 = 8m H ; L 2 = 2m H ; k = 0,75 ; R g = 1Ω e R L = 7Ω . Se v g = 54 2 cos 1000 tV , determinea) o valor eficaz de v o ;b) a potência méd