Uma alternativa ao filtro protótipo passa-faixa ilustrado na Figura P15.14 é fazer vo = 1 rad/s, R = 1 V e L = Q henrys.
a) Qual é o valor de C no filtro protótipo?
b) Qual é a função de transferência do filtro protótipo?
c) Use o circuito protótipo alternativo que acabamos de descrever para projetar um
filtro passivo passa-faixa que tenha um fator de qualidade de 16, uma frequência
central de 25 krad/s e uma impedância de 10 kV na ressonância.
d) Desenhe o diagrama do filtro modificado e identifique todos os componentes
e) Use os resultados obtidos no Problema 15.14 para escrever uma função de transferência do circuito modificado.
Passo 1
- Beleza, vamos com calma para encontrar nossa solução
- A função transferência é dada por
- O valores originais de R, L e C são dados por
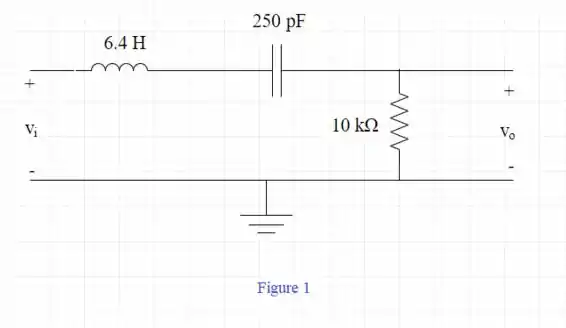
- A função de transferência H(s)’ do circuito é dada por
a frequência é dada por
a capacitância é dada por
Passo 2
substituindo os valores que já conhecemos
Determinando
onde R’ é o resistor dimensionado. Agora determinando
onde é a nova frequência após o dimensionamento dos elementos do circuito
Determinando agora o inductor redimensionado
a capacitância redimensionada C’
e a resistência R’
Passo 3
multiplicando o numerador e o denominador por (25000)²
Resposta
- Ver a figura