Em qual das amostras vista da Figura 11.58 é a maior a relutância ao longo da maior dimensão?
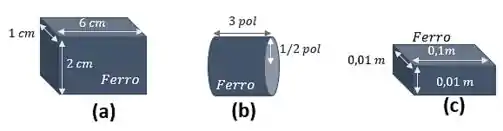
Figura 11.58
Passo 1
Fala galera do Responde aí, vamos para mais um probleminha!
Esse problema será um pouquinho 🤏 diferente dos que resolvemos até agora. Pois vamos explorar as relações de proporcionalidade da equação.
Como vamos trabalhar com a relutância, a equação escolhida para esse caso é descrita pela expressão:
Onde é uma constante que depende do material. Como todas as peças são feitas do mesmo material, a análise não vai depender de , pois o que vai mudar de uma peça para outra é a razão entre o comprimento e a área. Assim vamos trabalhar com a proporcionalidade entre:
Assim, a peça que apresentar a razão mais alta, é o que terá a maior relutância!
Passo 2
Vamos começar calculando a área de a cada uma das peças (Cuidado! Não se esqueça que o formato das peças é diferente, logo, a forma de calcular a área será diferente para uma delas):
Para que possamos comprar as peças, todas as áreas e comprimentos devem ser escritas na mesma unidade, então façamos as conversões…
Agora sim! 😊
Passo 3
Vamos calcular a razão para cada uma das peças:
Não se esqueça de reajustar as unidades quando há uma divisão ().
Resposta
Como vimos através do cálculo, a terceira peça é a que possui maior relutância.