Aplicando o teorema da superposição no circuito visto na Figura 18.115, determine a tensão .
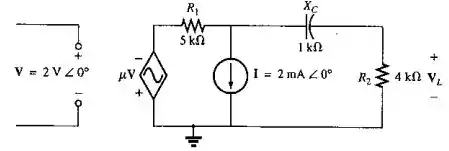
Passo 1
Opa, meus queridos, tudo bem? Vamos resolver essa questão rapidinho?
Dá uma olhada nas impedâncias deste circuito:
Podemos então aplicar o teorema da superposição. Lembrem-se que quando desligamos uma fonte de corrente, devemos substituí-la por um circuito aberto, e ao desligar uma fonte de tensão, devemos inserir um curto circuito em seu lugar.
Passo 2
Para começar, vamos desligar a fonte . Note que a tensão da fonte vai ser dividida entre as três impedâncias. Logo, a tensão em será dada por:
Note que a fonte está invertida e por isso adicionamos um sinal negativo na equação, beleza?
Em seguida, vamos desligar a fonte . Agora as impedâncias e estão em série e esta associação está em paralelo com . Logo, nós podemos calcular a corrente que passa por e usando o divisor de tensão:
Logo, a tensão na impedância pode ser calculada pela lei de Ohm. Devemos inverter o sinal de para respeitar o sentido da corrente:
Pelo teorema da superposição, só precisamos somar o resultado das duas análises: