Aqui está uma quarta maneira de calcular a energia de uma esfera uniformemente carregada: monte a esfera camada por camada, trazendo, de cada vez, uma carga infinitesimal de uma grande distância, espalhando-a uniformemente sobre a superfície e, consequentemente, aumentando o raio. Quanto trabalho é necessário para aumentar o raio em ? Integre isso para encontrar o trabalho necessário para criar a esfera inteira com raio e carga total .
Passo 1
Faaaala meu povo!! Como vocês estão? Bora lá resolver mais uma questãozinha?
Antes de tudo, vamos visualizar quais são as camadas que o enunciado sugere:
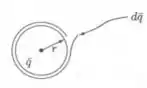
Agora, sobre o cálculo de energia, utilizaremos:
Passo 2
Nesse passo, observaremos a carga :
Passo 3
Agora aplicaremos em :
Aplicaremos a integração para encontrar :
Prontinho, pessoal!! Bora resolver mais uma questão juntos?