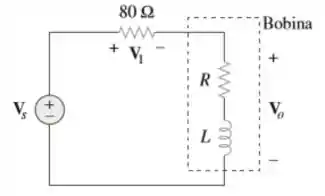
Uma bobina industrial é representada por um modelo que é uma associação em série de uma indutância L e uma resistência , conforme mostrado na Figura 9.90. Uma vez que um voltímetro CA mede apenas a magnitude de uma senoide, as medidas a seguir foram realizadas em quando o circuito opera no regime estacionário:

Use essas medidas para determinar os valores de e .

Desenvolvendo, chegamos a duas equações!

Dessas duas equações temos,

Aplicando isso para a equação de ,

Portanto,

Resolvendo o sistema de

Geramos que,