- Para cada circuito mostrado na Figura 9.129, determine o valor de R para a situação de máxima transferência de potência.
- Calcule o valor dessa potência para cada circuito.
Passo 1
Alô Alô, galerinha do responde ai, tudo bem?
Bora lá
- Vamos iniciar efetuando um curto circuito a fonte de tensão e iremos encontrar o valor do resistor de Thevenin
- Vamos redesenhar e encontrar a tensão de Thévenin
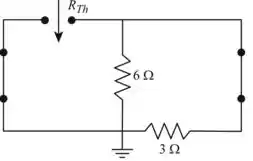
Figura 1
Passo 2
Vamos encontrar a resistência equivalente de Thévenin da rede
Portanto, o valor da resistência de Thévenin e o valor de R do circuito. Portanto, o valor de R é .
Passo 3
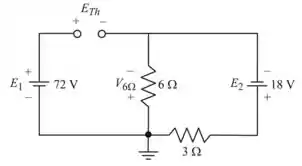
O valor é a soma de e da tensão através do resistor de .
Aplicando a regra do divisor de tensão e encontrando a tensão no resistor de
Aplicando o teorema da transferência de potência máxima , iremos encontrar a potência máxima para R.
Portanto, a potência máxima para R é de 882 W.
Passo 2
- Vamos iniciar efetuando um curto circuito a fonte de tensão e iremos encontrar o valor do resistor de Thevenin
- Aplicando o teorema da superposição iremos encontrar as tensões de Thévenin. Curto circuite a fonte de tensão e iremos encontrar o valor da tensão. Vamos redesenhar e encontrar a tensão de Thévenin
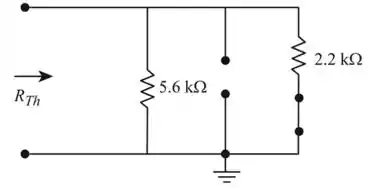
Figura 4
Vamos encontrar a resistência equivalente de Thévenin da rede
Portanto, o valor da resistência de Thévenin e o valor de R do circuito. Portanto, o valor de R é .
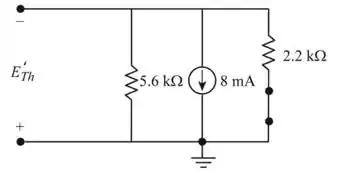
Figura 5
Aplicando a lei de Ohm iremos encontrar
Redesenhando
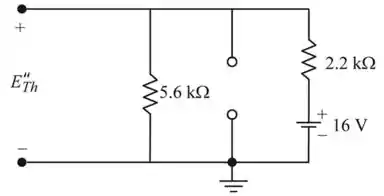
Figura 6
Aplicando a regra do divisor de tensão e encontrando
Analisando a figura 5 e 6. A fonte de tensão e corrente flui na direção oposta
Aplicando o teorema da transferência de potência máxima iremos encontrar a potência máxima para R.
Portanto, a potência máxima para R é de
Resposta
- Portanto, o valor da resistência de Thévenin e o valor de R do circuito. Portanto, o valor de R é .
- Portanto, a potência máxima para R é de 882 W.
- Portanto, o valor da resistência de Thévenin e o valor de R do circuito. Portanto, o valor de R é .
- Portanto, a potência máxima para R é de