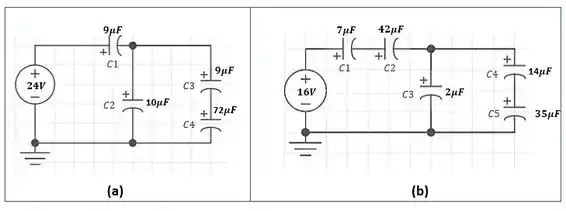
 Para cada configuração mostrada na Figura 10.106, determine a tensão entre os terminais de cada capacitor assim como a carga.
Para cada configuração mostrada na Figura 10.106, determine a tensão entre os terminais de cada capacitor assim como a carga.
Figura 10.106
Passo 1
Oi 😉, vamos para uma questão, essa com algumas particularidades, mas vamos resolver com calma 😊.
Da mesma forma que o problema anterior, vamos anotar as relações importantes para o problema:

Passo 2
a) Assim como fizemos no problema 45, vamos reduzir o circuito a um único valor de capacitância (capacitância total) e refazer os passos para determinar as tensões e cargas de cada elemento.
Começaremos então como os capacitores 3 e 4 que estão em série, logo, é dado por:
Agora estará em paralelo com , logo, será expresso por:
Essa junção, resulta em um circuito mais simples, que terá uma fonte e dois capacitores em série ( e ), sendo assim a será expressa por:
Sendo a tensão sobre correspondente a tensão da fonte.
Passo 3
Agora podemos calcular a carga correspondente ao , como:
Como é equivalente a ligação entre e , temos que:
𝑸𝟏
Passo 4
Agora que já temos algumas informações sobre a carga, podemos calcular a tensão sobre o , de forma que:
Agora vamos calcular a tensão sobre :
Como estará em paralelo com , a tensão sobre eles é a mesma, de forma que podemos escrever:
Consequentemente, a carga de corresponderá a:
Passo 5
Agora podemos calcular a carga sobre , pois como é o equivalente a dois capacitores que estão série, a carga sobre ele, será a carga dos capacitores individualmente.
Logo,
Passo 6
Por fim, a tensão sobre eles é de:
Passo 7
b) Para esse item, vamos trabalhar o mesmo raciocínio, achar e fazer o caminho reverso.
Assim temos:
Assim teremos:
Por último:
Passo 8
Sabemos que a tensão sobre é a tensão da fonte, assim podemos calcular a carga de .
Agora vamos fazer o caminho reverso, vamos separar os capacitores novamente.
Isso implica que:
Logo,
Vamos abrir mais um pouquinho…
Então,
Agora temos uma informação particular sobre dois capacitores:
Assim podemos exprimir o valor das tensões sobre os terminais de ambos:
Passo 9
Agora vamos abrir nos circuitos na parte correspondente a , como sabemos a carga dele, podemos calcular a tensão sobre ele:
Como , a tensão sobre eles é a mesma. Logo,
Assim, temos:
Passo 10
Por fim, temos , isso implica que:
Então vamos calcular , já que sabemos quanto vale a tensão para esse conjunto.
Sendo assim,
Passo 11
Por fim, temos a tensão sobre os terminais dos capacitores e expressar por:
Resposta
a) ; ; ; ; ; ; ;
b) ; ; ; ; ; ; ; ; ;