Para cada uma das formas de onda vistas na figura, determine o período, a frequência, o valor médio e o valor rms.
Passo 1
Primeiramente, vamos analisar a figura A.
Pela legenda, vemos que o lado de cada quadradinho vale:
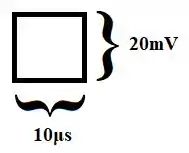
Passo 2
O período ocorre no seguinte intervalo de tempo:
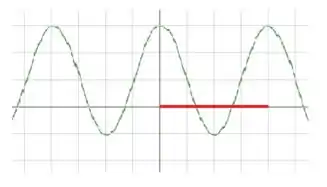
Ou seja, em 4 quadradinhos na horizontal. Assim, o período em é de .
Passo 3
Sabemos que o período é o inverso da frequência, ou seja:
Assim, substituindo valores temos:
Passo 4
Ao analisar os pontos máximo e mínimo da senoide, obtemos o valor médio . Veja:
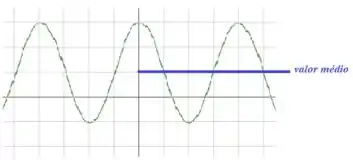
Como o valor médio tem o tamanho de um quadradinho na vertical, então podemos concluir que:
Passo 5
Sabemos que, SE a senoide estivesse alinhada de forma simétrica em relação a horizontal, teríamos que seu valor eficaz seria dado por:
Em que seria o valor de pico, ou seja, .
Abrindo a expressão anterior, temos que:
Obs: coloquei o zero para evidenciar uma senoide simétrica em relação ao eixo horizontal.
No nosso caso, vemos que a senoide está deslocada em um quadradinho na vertical. Assim, deduzimos que o valor eficaz é dado por:
Em que é o deslocamento vertical o qual a senoide está. No nosso caso, temos que a senoide está 1 quadradinho acima, ou seja, .
Assim, substituindo os valores, temos que:
Passo 6
Agora, para a figura B.
Pela legenda, vemos que o lado de cada quadradinho vale:
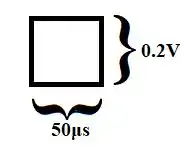
Passo 7
O período ocorre no seguinte intervalo de tempo:
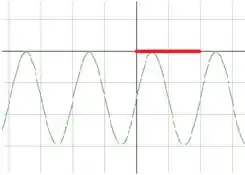
Ou seja, em 2 quadradinhos na horizontal. Assim, o período em é de .
Passo 8
Sabemos que o período é o inverso da frequência, ou seja:
Assim, substituindo valores temos:
Passo 9
Ao analisar os pontos máximo e mínimo da senoide, obtemos o valor médio . Veja:
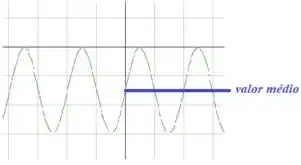
Como o valor médio tem o tamanho de um quadradinho e meio na vertical (no lado negativo em relação ao eixo horizontal), então podemos concluir que:
Passo 10
De forma análoga à figura A, determinaremos o valor eficaz da figura B.
Assim temos que:
Em que e
Portanto, temos:
Resposta
Figura A:
; ; ;
Figura B:
; ; ;