Calcule a capacitância total entre os pontos a e b dos circuitos da Figura 10.104.
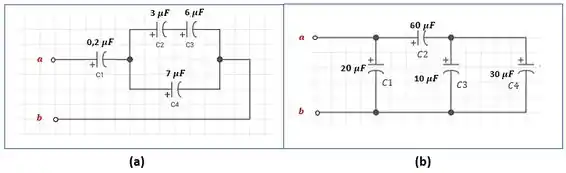
Figura 10.104
Passo 1
Fala aí galerinha!
Antes de começarmos a analisar o problema, vamos escrever as relações importantes para análise desses circuitos:

Agora que estamos totalmente equipados, vamos começar 😉!
Passo 2
a) O objetivo desse item é calcular a capacitância equivalente do circuito. Para isso vamos iniciar nossa análise pela malha destacada abaixo:
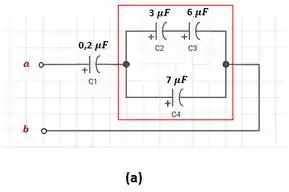
Onde e estão em série, logo, podemos calcular a capacitância equivalente ():
Inserindo as informações, temos:
Como e estavam em paralelo com , também estará em paralelo no circuito equivalente, por isso vamos calcular :
Inserindo as informações, temos:
Desta forma, estará em série com , assim a capacitância total será dada por:
Passo 3
b) Neste segundo caso, vamos iniciar nossa análise pela malha destacada abaixo:
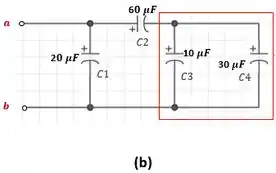
Onde e estão em paralelo, logo, podemos calcular a capacitância equivalente ():
Agora e estão em série, sendo assim será:
Por fim, estará em paralelo com ,logo, a capacitância total será de:
Viu?! Super simples 😊
Resposta
Para o circuito (a), a capacitância total é de:
Para o circuito (b), a capacitância total é de: