Calcule para o circuito magnético em série-paralelo da Figura 11.68 o valor de necessário para estabelecer um fluxo no entreferro
Passo 1
E aeeeee cara, vamos lá!
Nesse exercício, vamos precisar de várias informações diferentes para aplicarmos na fórmula da ffm, pra isso podemos montar essa uma tabela com os dados de cada uma das seções, de até
Preenchendo a tabela de acordo com os dados que já temos a princípio para cada seção:
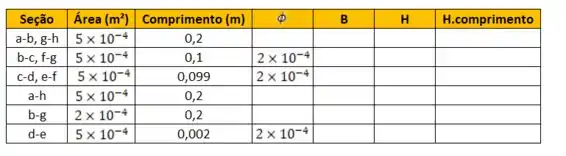
Vamos começar calculando o valor de , pode ser? Para isso, usamos a fórmula
Vamos lá!
Passo 2
Observando a tabela, vamos ter
Onde é o valor no gap que temos na figura ()
Então, vamos ver quanto vale esse geralzão aí:
Então a tabela fica assim, por enquanto
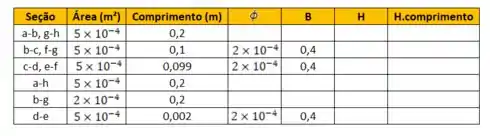
Passo 3
Belezinha, vamos calcular os H’s ok? Primeiro o do gap de ar:
Agora para calcular o das outras seções, precisamos olhar a figura 11.23 do seu livro. Lá vemos que o aço laminado em equivale a
Agora a tabela fica assim ó:
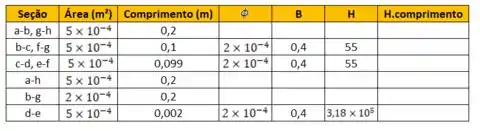
Passo 4
Agora vamos calcular o , que é outro dado que vamos precisar na fórmula da ffm
Para o gap de ar, temos
Já para as outras seções:
Ihuuu, a tabela ta ficando cada vez mais completinha:
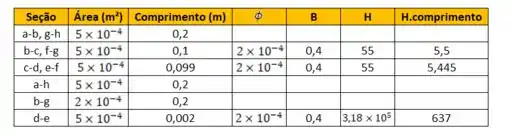
Passo 5
Agora temos dados suficientes para dar a volta no segundo laço do circuito, certo? Sabemos que a soma da ffm ali tem que ser 0, então
Substituindo os valores:
Então:
Mas temos que , então
Observando a figura 11.23 para o aço laminado, vemos que equivale a
Belezinha, já temos vários dados mas ainda faltam algumas coisas pra conseguirmos encontrar a famigerada corrente hehehehe
Passo 6
Sabemos que , certo? Como temos e , podemos encontrar :
Olha aí nossa tabela agora:
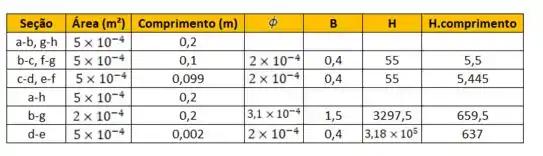
Passo 7
Temos que
Uhuuuu, então já encontramos , que no caso é
Boa, então temos e , podemos encontrar o :
E aí, vendo a figura 11.23 para o aço laminado, temos que em , o vale
Agora basta encontrar o nas linhas que faltam da tabela :D
Passo 8
Temos
E aí a nossa tabela fica completíssimaaaaa
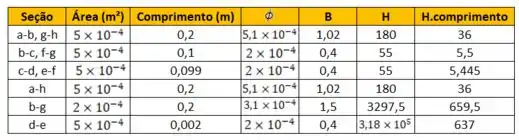
Nesse momento você deve estar pensando: QUE? A gente não queria a corrente???
Sim simmm, vamos calcular ela no próximo passo hehehe a coisa é que precisávamos de todooos esses dados pra aí conseguirmos a corrente I :P Vamos lá então
Passo 9
A corrente pode ser calculada a partir do laço esquerdo do circuito:
Substituindo os valores, sabendo que
Então:
Nossa, demorou mas acabou ahahhahaha