Calcule a corrente no circuito visto na Figura 18.118.
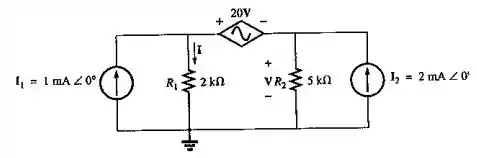
Passo 1
E aí, galera, prontos para resolver uma questão de circuitos?
Primeiramente, vamos listar as impedâncias deste circuito:
Vamos começar aplicando a LKT na malha central. Considere que a tensão na impedância se chama . Temos que:
(equação 1)
Em seguida, utilizaremos o teorema da superposição. Lembrem-se que quando desligamos uma fonte de corrente, devemos inserir um circuito aberto em seu lugar e ao desligar uma fonte de tensão, devemos substituí-la por um curto circuito.
Passo 2
Primeiro iremos considerar que a fonte de corrente está desligada. Neste caso, a corrente fornecida pela fonte vai se dividir entre as duas impedâncias. Logo, a corrente na impedância é dada por:
Pela lei de Ohm, temos a seguinte tensão na impedância :
(equação 2)
Igualando as equações 1 e 2, temos que:
Passo 3
Agora, iremos considerar que a fonte de corrente está desligada. Neste caso, a corrente fornecida pela fonte vai se dividir entre as duas impedâncias. Logo, a corrente na impedância é dada por:
Pela lei de Ohm e utilizando o resultado da equação 1:
Para finalizar, devemos somar os resultados das duas análises: