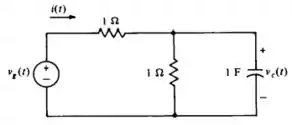
Calcule as respostas forçadas e a potência entregue a cada um dos resistores de no circuito do problema , se é a função do exercício
Passo 1
Nessa questão ele pede para calcular as respostas forçadas de e a potência entregue a cada um dos resistores de

Aposto que você tá com essa cara né? Hahaha fica tranquilo e vem.
Passo 2
Sabendo que,
Para encontrarmos as funções trigonométricas da série e Fourier devemos nos lembrar que,
Ficando,
A esquerda:
A direita:
Espero ter ajudado vocês, até a próxima pessoal.

Resposta
A esquerda:
A direita: