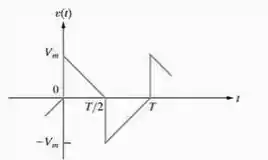
(a) A tensão tem simetria de meia onda. Portanto,
a v = 0 ; a k = b k = 0 , k
even
a k = 4 T ∫ 0 T / 2 V m - 2 V m T t c o s k ω o t d t , k
odd
b k = 4 T ∫ 0 T / 2 V m - 2 V m T t s i n k ω o t d t , k
odd
a k = 4 V m T ∫ 0 T / 2 c o s k ω o t d t - 8 V m T 2 ∫ 0 T / 2 t c o s k ω o t d t
= I n t 1 - I n t 2
I n t 1 = 4 V m T ∫ 0 T / 2 c o s k ω o t d t = 4 V m T ⋅ 1 k ω o s i n k ω o t 0 T / 2 = 0
I n t 2 = 8 V m T 2 c o s k ω o t k 2 ω o 2 + t s i n k ω o t k ω o 0 T / 2
= 8 V m T 2 1 k 2 ω o 2 ( c o s k π - 1 ) = - 16 V m k 2 4 π 2 = - 4 V m π 2 k 2 , k
odd
∴ a k = 4 V m π 2 k 2 , k
odd
b k = 4 V m T ∫ 0 T / 2 s i n k ω o t d t - 8 V m T 2 ∫ 0 T / 2 t s i n k ω o t d t
= I n t 1 - I n t 2
I n t 1 = 4 V m T ∫ 0 T / 2 s i n k ω o t d t = 4 V m T ⋅ - 1 k ω o c o s k ω o t 0 T / 2
= - 4 V m T k ω o [ c o s k π - 1 ] = 8 V m k ω o T = 4 V m π k
I n t 2 = 8 V m T 2 ∫ 0 T / 2 t s i n k ω o t d t
= 8 V m T 2 s i n k ω o t k 2 ω o 2 - t c o s k ω o t k ω o 0 T / 2
= 8 V m T 2 0 - T 2 k ω o c o s k π - 0 - 0 = 2 V m k π
∴ b k = 4 V m π k - 2 V m π k = 2 V m π k
∴ A k / Γ θ k = a k - j b k = 2 V m π k 2 π k - j 1
V m = 378 π m V
A k / - θ k _ = 756 k 2 π k - j 1 m V
v ( t ) = ∑ n = 1,3 , 5 ∞ A n c o s n ω o t - θ n
A 1 / - θ 1 = 896.20 ∠ - 57.52 ∘ m V
A 3 ∠ - θ 3 = 257.61 ∠ - 78.02 ∘ m V
A 5 ∠ - θ 5 = 152.42 ∠ - 82.74 ∘ m V
A 7 ∠ - θ 7 = 108.45 ∠ - 84.80 ∘ m V
A 9 ∠ - θ 9 = 84.21 ∠ - 85.95 ∘ m V
v ( t ) = 896.20 c o s ω o t - 57.52 ∘ + 257.61 c o s 3 ω o t - 78.02 ∘
+ 152.42 c o s 5 ω o t - 82.74 ∘ + 108.45 c o s 7 ω o t - 84.80 ∘
= + 84.21 c o s 9 ω o t - 85.95 ∘ +
....