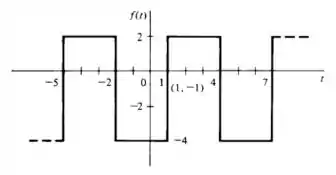
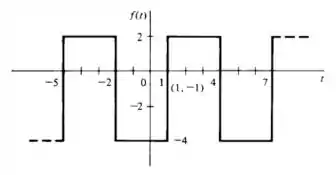
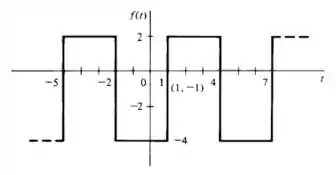
Calcule a série trigonométrica de Fourier para a função indicada, transladando inicialmente os eixos de forma a colocar a origem no ponto , e explorando a simetria que resultara. (nota: use os resultados dos Prob. 17.5 e 17.3(a))
Passo 1
Nessa questão ele pede para calcular a série trigonométrica de Fourier para a função indicada, transladando inicialmente os eixos de forma a colocar a origem no ponto , e explorando a simetria que resultara. (nota: use os resultados dos Problema 17.5 e 17.3(a))

Aposto que você tá com essa cara né? Hahaha fica tranquilo e vem.
Passo 2
Sabendo que,
Sabendo que,
Temos,
Ficando,
Espero ter ajudado, até próxima.

Resposta