Calcule a tensão no circuito visto na Figura 18.119.
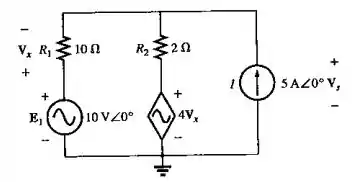
Passo 1
Falaaa pessoal, de boa? Vamos para mais uma questão de circuitos!
Primeiramente, vamos começar listando as impedâncias deste circuito:
Neste exercício, usaremos o teorema da superposição. Vale reforçar que o teorema não se aplica a fontes dependentes controladas por uma variável determinada pelo circuito, como o caso da fonte de tensão .
Lembrem-se também que quando desligamos uma fonte de corrente, devemos inserir um circuito aberto em seu lugar e ao desligar uma fonte de tensão, devemos substituí-la por um curto circuito, beleza?
Inicialmente, vamos imaginar que a fonte está desligada. Considere que uma corrente passe pela malha da esquerda. Aplicando a LKT nesta malha, teremos que:
(equação 1)
Substituindo na equação 1, obtemos:
Aplicando a LKT na malha externa, teremos que:
Passo 2
Em seguida, vamos ligar a fonte e imaginar que a fonte está desligada. Pelo método das tensões dos nós, teremos que:
Note que consideramos que as correntes estão “entrando” nos nós, isto é, no sentido da queda de tensão.
Como .
Por fim, devemos somar os resultados das duas análises: