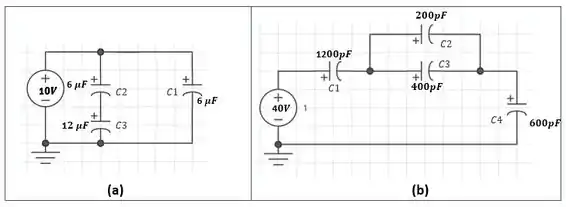
 Calcule a tensão entre os terminais dos capacitores e sua carga para os circuitos vistos na Figura 10.105.
Calcule a tensão entre os terminais dos capacitores e sua carga para os circuitos vistos na Figura 10.105.
Figura 10.105
Passo 1
Olá pessoal, vamos para mais um exercício da seção 10.13.
Assim como no problema anterior, vamos anotar as relações importantes para o problema:

Passo 2
a) Assim como no problema anterior, destaquem as malhas pelo qual vamos passar na análise, esse será o treinamento de você ok?!
Como na malha mais externa, só temos a fonte e o capacitor, em paralelo, a tensão sobre o capacitor 1 é igual à da fonte:
𝑉𝑐1
Sua carga será expressa pela equação:
𝑄1
Passo 3
Se olharmos a malha a esquerda, veremos dois capacitores em série, de forma que estará sobre a tensão da fonte (caso semelhante ao do ). Então vamos calcular :
Sobre a tensão de 10 V. Com essa informação podemos calcular a carga de .
Como os capacitores estão em série, temos a condição descrita no passo 1:
Logo:
𝑄𝑐2
Passo 4
Conhecendo a carga e a capacitância, podemos calcular a tensão sobre cada um dos capacitores:
Passo 5
b) Mesmo os itens sendo distintos entre si, vamos fazer uma análise semelhante. Vamos calcular a capacitância total do circuito. Começando com e , que estão em paralelo. Sendo assim:
Assim reduzimos o circuito a uma malha, com , e em série. A capacitância total, será de:
Passo 6
Agora que achamos a capacitância total, a tensão que atua sobre os terminais de é a tensão da fonte, logo, . Sendo assim, podemos calcular a carga total., expressa por:
Como equivale a , e , e eles estão ligados em série:
Logo,
Obs.:
Passo 7
Agora podemos calcular o valor da tensão sobre os capacitores , e .
Passo 8
Como os capacitores e estão em paralelo, a tensão sobre eles é mesma, sendo assim:
Com essa informação podemos calcular a carga de cada um deles.
Resposta
a) ; ; ; ;
b) ; ; ;
; ;