 14. Calcule as tensões máximas de operação dos capacitores dos problemas 12 e 13, considerando que existe uma relação linear entre a tensão de ruptura e a espessura do dielétrico.
14. Calcule as tensões máximas de operação dos capacitores dos problemas 12 e 13, considerando que existe uma relação linear entre a tensão de ruptura e a espessura do dielétrico.
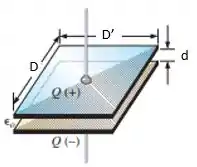
Ilustração de um capacitor de placas paralelas
Passo 1
Oi galerinha, vamos dar início a mais uma seção deste capítulo.
Vamos iniciar anotando as informações dos problemas citados:
- problema 12
- problema 13
O dielétrico é o ar, que tem rigidez dielétrica igual a (valor tabelado)
O dielétrico é a baquelite, que tem rigidez dielétrica igual a (valor tabelado)
Nesse primeiro passo é importante realizar as conversões das unidades de acordo com o SI. Isso nos poupa trabalho na hora de fazer a conta e evita erros.
Passo 2
Problemas desse tipo se resumem a encontrar a equação relaciona as grandezas que conhecemos com aquelas que vamos determinar. Por isso, escolheremos a equação onde tensão máxima aplicada, é descrita pelo produto da rigidez dielétrica, pela espessura do dielétrico.
Ao inserir as informações na equação, temos:
Viu? Super simples! 😄
Resposta
Então as tensões máximas são dadas por: