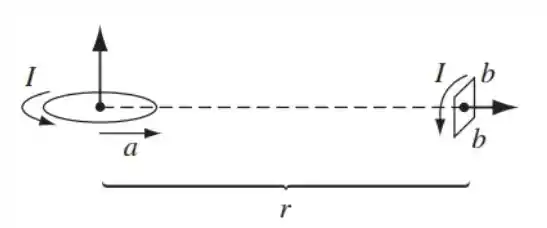
Calcule o torque exercido na espira quadrada mostrada na Fig. 6.6, devido à espira circular (suponha que r seja muito maior que a ou b). Se a espira quadrada estiver livre para girar, qual será sua orientação de equilíbrio?
Passo 1
Vocês estão prontos crianças??
Estamos capitão??
Eu não ouvi direitoooo...
Estamos capitãoooo haha
Bora resolver essa comigoooo??
O torque pode ser definido como a tendência de uma força para girar um objeto em torno de algum eixo.
Vamos calcular o torque exercido na espira quadrada devido à espira circular.
O momento magnético da espira circular é e está na direção do eixo z, ou seja,
O momento magnético da espira quadrada está na direção y, ou seja,
Então o torque na malha quadrada é
O produto escalar de quaisquer dois vetores diferentes é igual a zero
Passo 2
Agora sim podemos substituir na expressão 1
Pela regra da mão direita, temos que
Passo 3
O momento magnético para a espira circular é
Substituindo na segunda expressão
Para que a espira quadrada esteja em equilíbrio, o torque líquido deve ser zero. Então a orientação é de loop quadrado é direção descendente .
Resposta
Portanto, o torque na espira quadrada devido à espira circular é