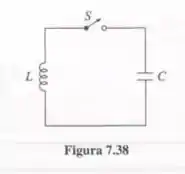
Um capacitor C é carregado até um potencial V e ligado a um indutor L, como mostra esquematicamente Figura 7.38. No tempo t=0 a chave S é fechada. Encontre a corrente no circuito, como função de tempo. Como a sua resposta se altera se um resistor R for incluído em série com C e L?
Passo 1
Olá pessoal, bora para mais uma!?
Como a corrente I é horária, temos que:
Onde, temos que é a carga no capacitor e , ou seja:
Vamos definir , ou seja:
A solução da EDO acima é conhecida. Então temos que:
Porém sabemos que em t=0, Q=CV, assim:
Ou seja, A=CV. Temos também que:
Em t=0, temos que I=0, logo B tem que ser nulo. Então temos que Q(t), pode ser expresso como:
Passo 2
Agora que temos Q(t), podemos encontrar I. ou seja:
Substituindo temos que:
Ressaltando que se colocarmos um resistor em série como mencionado no enunciado. Teremos uma oscilação amortecida.
Assim, finalizamos mais uma! Até a próxima!