O capacitor da Figura 10.100 está carregado inicialmente com 3V, com polaridade mostrada na figura.
a) Escreva as expressões matemáticas para a tensão e a corrente depois que a chave é fechada.
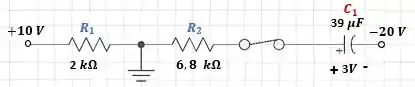
Figura 10.100
Passo 1
Hello guys! Voltamos a estrutura abertinha dos circuitos, mas já estamos feras nisso 😉!
Mais uma vez, vou chamar a atenção para o fato de o capacitor estar carregado.
Vamos anotar as informações sobre o problema:
Façam as conversões de unidade, nesta etapa! Evitem os erros!
Passo 2
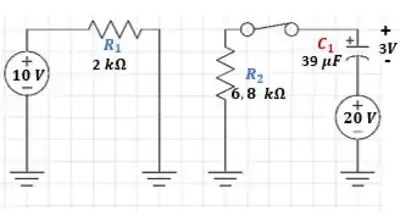
Como nossa análise tem foco no capacitor, vamos manter nos concentrar no circuito 2. Sendo assim, vamos reescrever as informações relevantes ao problema:
Passo 3
Com as informações em mãos, vamos determinar a constante de tempo:
Assim podemos escrever as equações e , lembrando que o capacitor já estava carregado. Desta forma, temos:
e,
Passo 4
Esboce os gráficos de e : (obs. Os gráficos foram construídos com o software gratuito Graph)
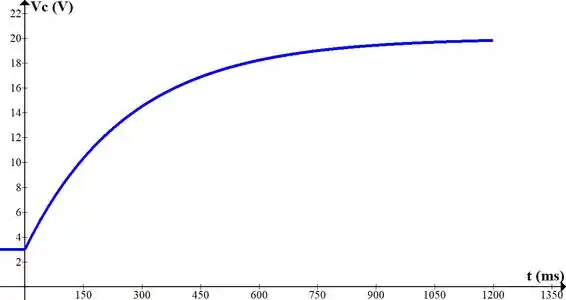
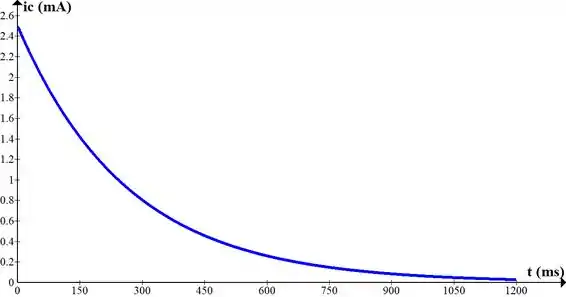
Resposta
a) ;