27. O capacitor da figura 10.89 está carregado inicialmente com 12 V, com a polaridade indicada.
a) Determine a expressões matemáticas para a tensão e a corrente depois que a chave é fechada.
b) Esboce as formas de onda de e .
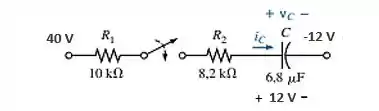 Figura 10.89
Figura 10.89
Passo 1
E aí galera, esse probleminha tem uma estrutura parecida com o problema 20, porém neste caso o capacitor está carregado.
Em primeiro lugar, vamos anotar informações do problema:
Lembrando que a diferença de potencial será a soma dos valores mostrados na figura.
Passo 2
Antes de iniciar a análise dos itens, vamos primeiro calcular a resistência equivalente, pois com a prática, já sabemos que precisamos dela para determinar a constante de tempo.
Passo 3
Como próximo passo, temos que determinar a constante de tempo do circuito.
Mesma receitinha 😋…
Passo 4
a) Como primeiro passo nesse item, devemos prestar atenção ao fato de o capacitor estar inicialmente carregado, logo, a expressão para tem que levar em consideração .
Agora com todas as informações em mãos, podemos escrever como:
Passo 5
Ainda no item a – A expressão geral para corrente, neste caso, é escrita como:
Com todas as informações em mãos, podemos escrever:
Assim temos escrita como:
Agora, basta inserir as informações.
Fica a dica: Não deixem de relembrar as equações escritas na seção do livro, pois quando mudam os parâmetros, as equações tendem a sofrer alterações.
Passo 6
b) Esboce as formas de onda de e .
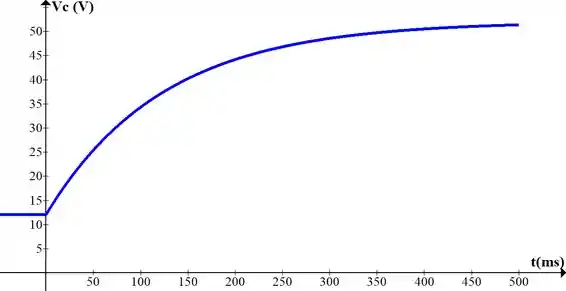
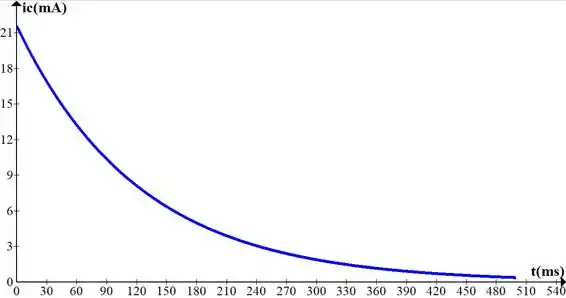
Resposta
a) ;