O capacitor da Figura 10.98 está carregado inicialmente com 4V, com polaridade mostrada na figura.
a) Escreva as expressões matemáticas para a tensão e a corrente depois que a chave é fechada.
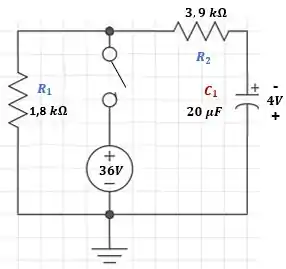
Figura 10.98
Passo 1
Oi galerinha, vamos a mais um probleminha daqueles de dar dor de cabeça. Vamos resolver do mesmo jeitinho, com passinhos de tartaruga 😊
Vamos anotar as informações sobre o problema:
Passo 2
Quem se esqueceu das aplicações do teorema de Thévenin, para rapinho e dê uma relembrada lá na seção 10.11.
Aplicando o teorema sobre o capacitor, temos:
Como nosso R’ não está representado no circuito, vamos adotá-lo como nulo. Dessa forma temos:
Como há apenas uma fonte, temos:
Passo 3
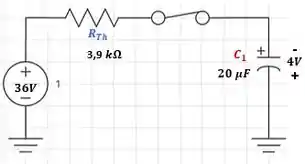 Agora nosso circuito pode ser reescrito como:
Agora nosso circuito pode ser reescrito como:
Já facilitou bastante nossa vida 😉. Assim podemos exprimir com mais facilidade as informações que precisamos para escrever as equações matemáticas de e .
Passo 4
Voltamos a nossa receitinha 😋. Vamos determinar a constante de tempo:
Assim podemos escrever as equações e , lembrando que o capacitor já estava carregado. Desta forma, temos:
e,
Passo 5
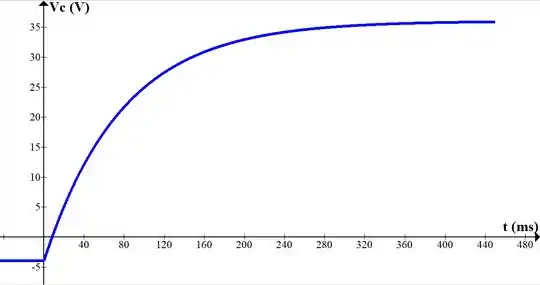
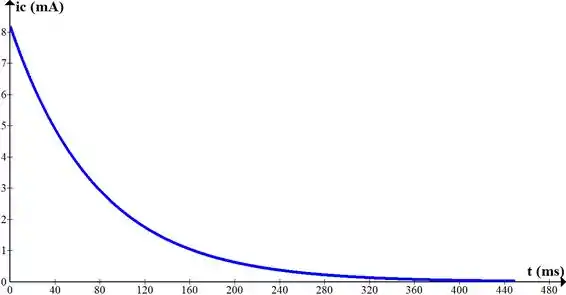
Resposta
a) ;