- A carga está em repouso na origem no sistema S; a carga passa à velocidade v em uma trajetória paralela ao eixo x, mas em . Qual é a força eletromagnética sobre quando ela cruza o eixo y.
- Agora estude o mesmo problema a partir do sistema que se move para a direita à velocidade v. Qual é força sobre quando passa pelo eixo ? [faça de duas maneiras: (i) usando a sua resposta para (a) transformando a força; (ii) calculando os campos em e usando a lei de força de Lorentz.]
Passo 1
Faaaaaala, galera... Tranquileba??
Para a)
Fazendo um esboço da situação dita no enunciado, temos:
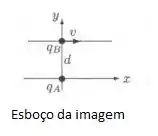
Sabemos que a força eletromagnética é:
Temos pela lei de bio savart:
Veja que , logo
E o campo que a carga a exerce na b é:
Assim:
Brincadeiras à parte, bora pro próximo passo?!
Passo 2
Obrigado por vir.
Para b)
(i)
Temos da eq. 12.68
Assim:
Passo 3
(ii)
Temos pela equação 12.92:
Com ângulo de 90°, temos:
E não havendo força magnética, temos:
Resposta
Para a)
Para b)