As cargas de uma fábrica ligada a um sistema de 1000 V, 60 Hz, são as seguintes:
20 kW para aquecimento (fator de potência unitário)
10 kW () para motores de indução (fator de potência 0,7 atrasado)
5 kW para iluminação (fator de potência 0,85 atrasado)
a. Desenhe o triângulo de potência para a carga total.
b. Determine a capacitância necessária para tornar o fator de potência total igual a 1.
c. Calcule a diferença entre as correntes totais no sistema compensado e no sistema não-compensado.
Passo 1
Bom dia, boa tarde, boa noite meu povo, tudo certo? Bora resolver mais uma questão?
Primeiramente encontraremos os valores para cada carga:
Para carga 1:
Para carga 2:
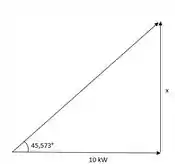
Para carga 3:
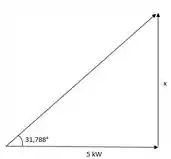
Agora calcularemos as potências para então montarmos o triângulo de potências:
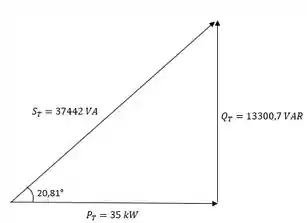
Passo 2
Para determinarmos a capacitância, temos primeiramente que:
Segundamente, calcularemos
Agora com os valores encontrados acima, podemos finalmente calcular a capacitância:
Passo 3
No sistema não-compensado temos:
No sistema compensado, temos:
Sendo assim, teremos podemos observar que a diferença entre as correntes nesse caso é:
E é isso pessoal, finalizamos essa!!!! Vamos juntos resolver mais uma?
Resposta
a.
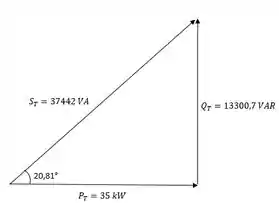
b. .
c. .