Uma casca esférica oca tem a densidade de carga para o caso .
Na região (Figura 2.25). Encontre o campo elétrico nas três regiões: (i) , (ii) , (iii) . Faça um gráfico de como função de .
Passo 1
Falaaa, tudo belezaa?? Para acharmos o campo elétrico com a lei de Gauss usamos a fórmula abaixo:
Quer dizer que a integral do campo elétrico em uma superfície fechada é igual a carga envolvida dividida por uma constante. O que precisamos agora é definir a superfície e a carga envolvida. Bora lá!!!
Passo 2
Vamos interpretar a imagem a qual o enunciado se refere:
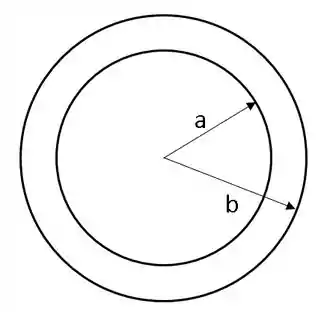
Podemos notar logo de cara que quando o , a superfície gaussiana será menor que a casca esférica. Então, não teremos carga envolvida e o campo elétrico será zero.
Passo 3
Agora para a segunda parte da questão teremos carga envolvida.
Então, temos que considerar a superfície gaussiana que será a área superfície de uma esfera. E a densidade foi dada pelo enunciado, o que importa no caso de é que os limites da carga envolvida são de até . Calculando a carga envolvida como uma integral esférica:
Substituindo na lei de Gauss.
Passo 4
Quando quer dizer que envolvemos toda a casca esférica. Sendo assim, os limites da integral da carga envolvida são de até . Calculando a carga envolvida:
Substituindo na Lei de Gauss.
Passo 5
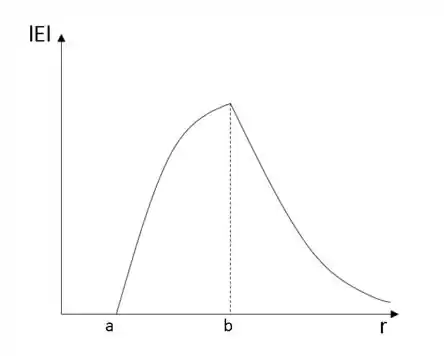
O gráfico de em relação a pode ser analisado abaixo: