Uma chapa grossa que se estende de a tem uma corrente volumétrica de densidade uniforme (Figura 5.41). Encontre o campo magnético como função de z, tanto dentro quanto fora da chapa.
Passo 1
Faaala, galerinha!! Como vocês estão? Partiu resolver mais uma questãozinha?
A esquemática dessa questão está mostrada abaixo:
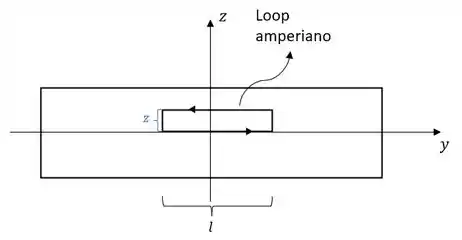
A partir da regra da mão direita, vemos que o campo aponta para a direção , quando . Quando , o campo aponta para a direção .
Além disso, a partir dessa regra mencionada e da esquemática apresentada, vemos também que quando , o campo B também será zero.
Passo 2
Utilizando o loop amperiano mostrado na esquemática do passo 1, podemos desenvolver as relações que mostrarão o valor do campo:
Se ,
Portanto, o campo é:
Prontinho, pessoal!! Bora resolver mais uma questão juntos?