A chave do circuito visto na figura 12.84 foi deixada aberta por um longo tempo e depois fechada em
a) Escreva uma expressão matemática para a corrente e a tensão após a chave ser fechada
b) Esboce a forma de onda e desde o momento em que a chave for fechada até que o circuito atinja o estado estacionário
Passo 1
Olá oláá, vamos lá pra mais um hehehe
A primeira coisa que dá pra gente pensar ao ver o circuito, é em uma transferência de fontes: temos uma fonte de corrente em paralelo com um resistor, podemos transformar isso em uma fonte de tensão em série com o resistor.
O valor da nova fonte vai ser
Passo 2
a) A expressão de é dada por
Vamos calcular os valores que precisamos para substituir aí, fechou?
Primeiramente vamos encontrar
Então
Passo 3
Agora vamos encontrar : ele vai ser a corrente no instante antes que a chave seja fechada
O pode ser encontrado assim olha, a partir do momento que a chave fecha (a parte direita do circuito é desconsiderada quando a chave fecha, sacou?):
Passo 4
Agora vamos substituir os valores
Então
E encontramos a expressão :D agora vamos lá para
Passo 5
A expressão de vai ser dada por
Vamos encontrar . Pela LKT, temos:
Onde , então:
E enfimmmm a expressão de é
Passo 6
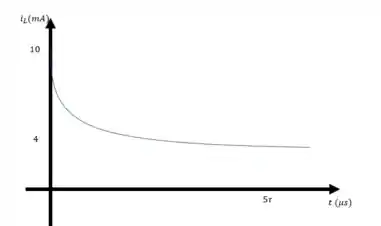
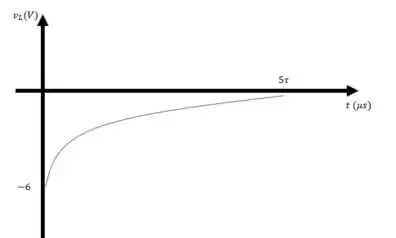
b) Vamos lá plotar os gráficos
Sabemos que
Analisando algebricamente, quando , temos e
Quando , temos e
Então os gráficos ficam assim
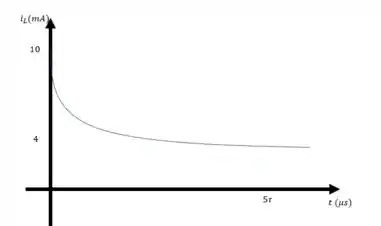
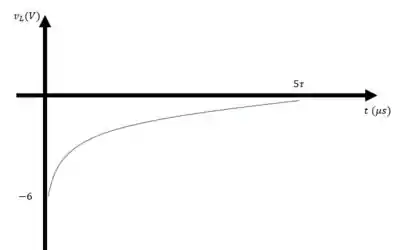
Resposta
a)
b)