A chave do circuito visto na figura 12.83 foi fechada por um longo tempo e depois aberta em
a) Escreva uma expressão matemática para a corrente e a tensão após a chave ser aberta
b) Esboce as formas de onda de e desde o momento em que a chave foi aberta até que o circuito atinja o estado estacionário.
Passo 1
Oieeee, tudo certo? Vamos lá pra mais um exercício
a) A expressão de é dada por
Vamos calcular os valores que precisamos para substituir aí, fechou?
Primeiramente vamos encontrar
Onde
Então
Passo 2
Agora vamos encontrar : ele vai ser a corrente no instante antes que a chave seja aberta
O pode ser encontrado assim olha, a partir do momento que a chave abre:
Passo 3
Agora vamos substituir os valores
Então
E encontramos a expressão :D agora vamos lá para
Passo 4
A expressão de vai ser dada por
Vamos encontrar . Pela LKT, temos:
Onde , então:
E enfimmmm a expressão de é
Passo 5
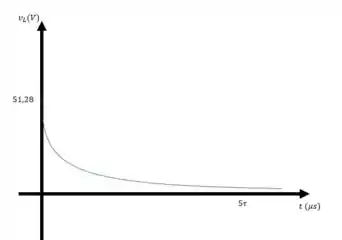
b) Vamos lá plotar os gráficos
Sabemos que
Analisando algebricamente, quando , temos e
Quando , temos e
Então os gráficos ficam assim

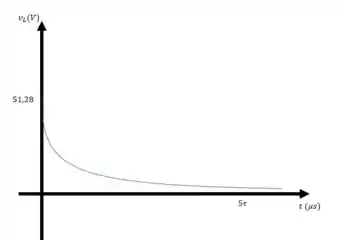
Resposta
a)
b)