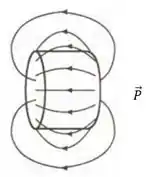
Um cilindro curto de raio e comprimento L tem uma polarização uniforme “congelada” P, paralela ao eixo. Encontre a carga de polarização e esboce o campo elétrico (i) para , (ii) para e (iii) para . [Este dispositivo é conhecido como barra de letreto; é o análogo elétrico de uma barra magnética. Na prática, somente materiais muito especiais – titanato de bário é o exemplo mais “conhecido” – mantêm uma polarização elétrica permanente. Por isso você não pode comprar eletretos em uma loja de brinquedos.]
Passo 1
Faaaala galera!! Como vocês estão? Bora lá resolver mais uma questãozinha?
Nesse probleminha aqui, como temos uma polarização uniforme “congelada” (P), e que é paralela ao eixo, as seguintes expressões dizem respeito aos valores das cargas de polarização nos casos descritos no enunciado:
Para a expressão de acima, vale lembrarmos que com o sinal de + em uma extremidade, o P aponta “em direção a”; com o sinal de – na outra extremidade, o P aponta para “longe de”.
Passo 2
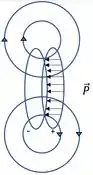
No caso (i), temos . Nesse caso, temos a figura feita como um dipolo, como mostrado abaixo:
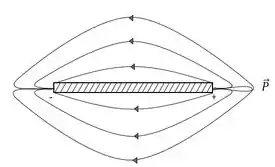
Então as extremidades parecem cargas puntiformes, e a coisa toda é como um dipolo físico, de comprimento L e carga .
Passo 3
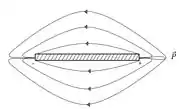
No caso (ii), temos , sendo representada na figura esquemática abaixo:
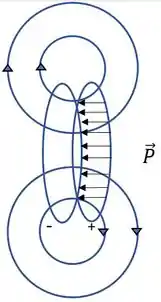
Então, é como um capacitor circular de placas paralelas. O campo nesse caso é quase uniforme; e o campo nas beiras é não uniforme.
É isso então galerinha!! Bora pra próxima questãoo!!
Passo 4
No caso (iii), temos , e, portanto, sua representação se dá como abaixo:
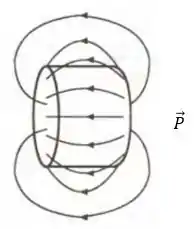
Resposta
(i):
(ii):
(iii):