Para o circuito da Figura 10.82:
a) Determine a constante de tempo do circuito.
b) Escreva a equação matemática para a tensão depois que a chave é fechada.
c)Determine a tensão depois de transcorrida uma, três e cinco constantes de tempo.
d) escreva as equações para corrente e a tensão .
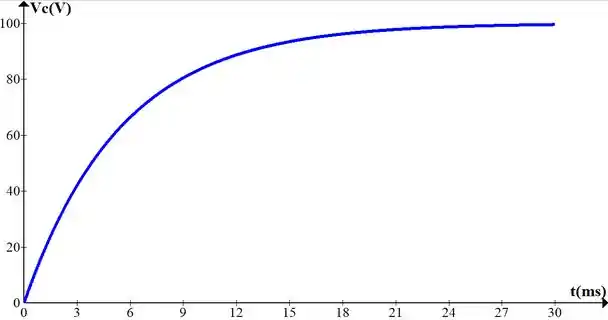
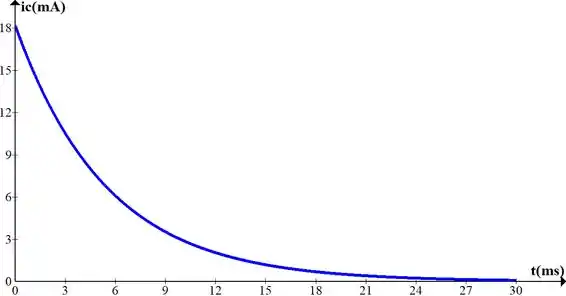
e) Faça um esboço das formas de onda de e .
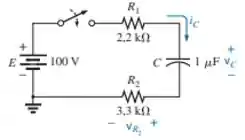
Figura 10.82
Passo 1
Oi galera do Responde aí, estamos aqui com mais uma questão de circuitos elétricos, naquele mesmo estilo das anteriores, o que é bom para nós 😉.
Vamos anotar as informações do problema:
Lembrando mais uma vez! Faça as conversões nesta etapa, isso irá facilitar bastante a sua conta.
Passo 2
Novamente, temos os mesmos itens das questões anteriores desta mesma seção, então já estamos familiarizados com as equações. Porém há uma particularidade nesta, há dois resistores!

Mas não é motivo para desespero, esse será um problema fácil de resolver 😎😎!
a) Para calcular a constante de tempo através da relação abaixo, precisamos de informação sobre a resistência, mas qual resistência é essa?
A resistência que procuramos é o do circuito. Como há dois resistores neste circuito e estão em série 👌, por isso basta que calcular a resistência equivalente.
Lembrando que resistores em série, a resistência equivalente é a soma das resistências de cada um deles.
Passo 3
Agora podemos seguir com a vida 😉, e calcular a constante de tempo:
Passo 4
b) A expressão matemática para a tensão para a constante de tempo de terminada no item anterior, é dada por:
Perceberam?! Voltamos para mesma receitinha dos problemas anteriores.
Passo 5
c) Agora vamos determinar a tensão para os tempos .
Utilizando a mesma lógica, teremos:
Dessa forma, o , será:
Passo 6
d) Escrever a equação para a corrente . De forma análoga ao que foi feito para a tensão , vamos inserir as informações que temos, na equação geral da corrente, que é representada por:
Desta forma, obtemos:
Passo 7
Ainda no mesmo item, o livro pede que a expressão matemática para , (Essa etapa se modifica ligeiramente dos problemas anteriores, por conta da quantidade de resistores, mas não deixa de ser a utilização da lei de Ohm), então inserindo as informações na equação, temos:
Passo 8
e) Faça um esboço das formas de onda de e . Esse esboço foi construído no software Graph, onde foram inseridas as equações de e obtidas nos itens anteriores
Resposta
a)
b)
c) ; ;
d) ;