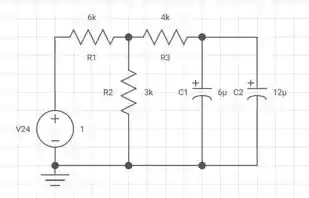
52. Para o circuito da Figura 10.109:
a) Determine a energia armazenada por cada capacitor no estado estacionário.
 b) Repita o item (a) para o caso de os capacitores estarem conectados em série.
b) Repita o item (a) para o caso de os capacitores estarem conectados em série.
Figura 10.109
Passo 1
Oi galerinha, último probleminha da seção, aquele para queimar o cérebro um pouquinho.
Vamos anotar as informações:
Não se esqueçam de fazer as conversões necessárias para o problema.
Passo 2
a) A energia armazenada em um capacitor é descrita por:
Isso nos indica que primeiramente, devemos calcular a tensão sobre os terminais dos capacitores. Como então a tensão sobre ambos é a mesma, logo só precisamos calcular a tensão sobre um deles. Para simplificar esse caminho, vamos calcular , que estão em paralelo:
Logo, temos:
Assim podemos desenhar o circuito como:
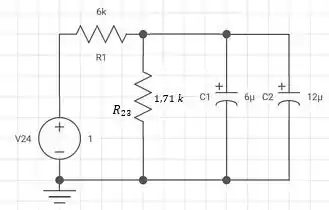
Já está com uma carinha mais amigável, não acham?
Passo 3
No “novo” circuito, temos que , então só precisamos determinar a tesão sobre o , como isso temos:
Logo,
Então temos:
Passo 4
Agora possuímos todas as informações para calcular a energia armazenadas pelos capacitores. Sendo:
e
Caso tenha ficado dúvidas, retorne os problemas da seção 11.13, toda discussão sobre a tensão nos capacitores é mais detalhada lá.
Passo 5
b) Agora para o caso de os capacitores estarem em série, podemos calcular a capacitância total do circuito ().
Assim podemos desenhar o circuito como:
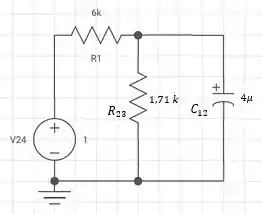
Muito mais simples, não é mesmo? Dessa forma temos:
Passo 6
Com essa informação podemos calcular a carga de .
Como e estão em série, temos:
Passo 7
A energia também pode ser escrita em função da carga do capacitor, pela equação:
Logo, temos;
Resposta
a) ;
b) ;