Enunciado
Elétrica - Introdução a Análise de Circuitos, de Boylestad- Ed: 10º - Capítulo 10.Problemas - Ex. 36
Para o circuito da Figura 10.96
a) Determine as expressões matemáticas para o comportamento transitório da tensão e da corrente depois que a chave é fechada.
b) Esboce as formas de onda para e
Passo 1
Para esse circuito vamos fazer igual fizemos no exercício 35. Vamos calcular o equivalente de thévenin para esse circuito à partir dos terminais do capacitor. Para esse equivalente, a R1 fica em paralelo com R2 Então, para calcular o Rth:
Feito isso, para calcularmos a tensão nos terminais do capacitor (Vth) conseguimos observar que é a mesma tensão no resistor R2, então basta fazer um divisor de tensão entre o resistor de R1 e R2 com a fonte:
Por último nesse passo, vamos calcular o , lembrando que o R é o Rth + R4 no momento que a chave fecha, e C foi dado no problema:
Com isso calculado já conseguimos extrair a tensão no capacitor! Vamos fazer isso no próximo passo.
Passo 2
Com a tensão no capacitor conhecida (Vth) e com conseguimos expressar a tensão no capacitor variando no tempo. Vamos escrever a equação primeiro:
Substituindo os valores conhecidos:
Fazendo esse equivalente de thévenin ficou mole, não foi?
Passo 3
Agora para fazer a expressão da corrente basta escrevermos a equação dela e substituir nossos valores. Vamos escrever ela primeiro:
Substituindo os valores que conhecemos, temos a expressão da corrente:
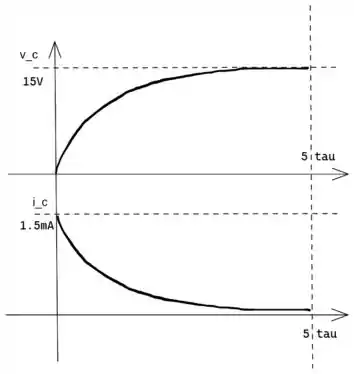
Pronto! Agora só falta desenhar as formas de onda
Passo 4
Conhecemos o valor máximo e mínimo de tensão, basta desenhar a curva característica de ic e vc respeitando esses limites:
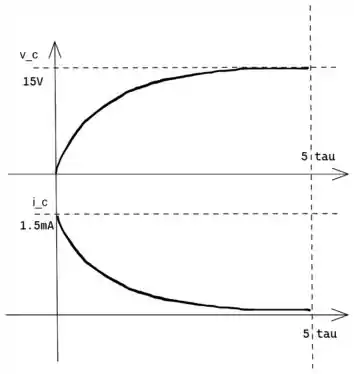
Resposta
a) ,
b)
