Para o circuito da Figura 15.119:
a. Determine a impedância na forma polar.
b. Construa o diagrama de impedâncias.
c. Determine a corrente e as tensões e em forma fasorial
d. Construa o diagrama de fasores para as tensões , e para a corrente
e. Verifique a valideda da lei de Kirchhoff para tensões ao longo da malha fechada
f. Calcule a potência média fornecida ao circuito
g. Calcule o fator de potência do circuito indicando se ele é adiantado ou atrasado
h. Determine as expressões senoidais para as tensões e correntes sendo a frequência 60 Hz
i. plote as formas de ondas das tensões e da corrente no mesmo gráfico
Passo 1
Faaaaaala galeeera
podemos calcular dessa forma
Passo 2

Passo 3
Começaremos com a corrente
(para calcular o ângulo usamos )
Agora a tensão
Para a tensão
Passo 4
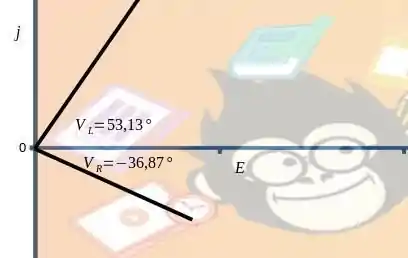
Passo 5
Vamos verificar a seguinte igualdade
Primeiro usaremos algumas propriedades anteriores
mais um detalhe
Belezinha até aqui?
Lembra que calculamos como ?
bora substituir de novo
simplificando
a igualdade é verdadeira
Caso substituíssemos os números, o valor também seria verdadeiro, porque usamos essas definições na hora de calcular os valores
Passo 6
Lembra como calcular a potência média?
Essa aqui é uma das formas
Passo 7
Vamos calcular o fator de potência
Passo 8
Para escrever as expressões senoidais, precisamos de mais uma informação
o valor de
Agora já estamos prontos
Passo 9
As formas de ondas serão baseadas nas equações do Passo 8, olhe a Figura 15.39, a diferença é que será os valores do passo anterior.
Resposta
a.
b. Resposta no passo 2
c.
d. Resposta no Passo 4
e. Resposta no passo 5
f.
g.
h.
i. Resposta no Passo 9