Para o circuito da Figura 12.72
a) Escreva as expressões matemáticas para a corrente e a tensão após a chave ser fechada.
b) Esboce as formas de onda de e entre o momento que a chave é fechada e o estado estacionário
Passo 1
Bora pra mais exercício de circuito RL. Esse exercício é muito parecido com o exercício 17 caso você já tenha feito! Se não tiver, não tem problema nenhum, vem comigo que vai dar bom
Para esse exercício vamos converter a fonte de corrente em uma de tensão para facilitar a nossa análise. Para converter basta multiplicar a corrente da fonte pela resistência em paralelo, transformar a fonte de corrente em uma de tensão e colocar em série. Vamos calcular:
Subtraindo essa fonte que convertemos à fonte que já está no circuito ficamos com uma fonte só, facilitando mais ainda pra gente:
Ficamos com esse circuito aqui, com , e
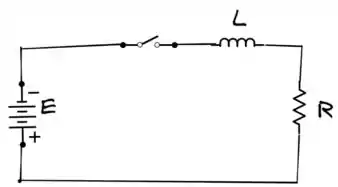
Passo 2
Vamos calcular o agora. Se você se lembra da teoria, no circuito indutivo é . Quando a chave se fecha a resistência é R1+R2, então:
Nesse circuito como temos uma corrente inicial de 3mA indicada no circuito, devemos considerar ela para escrever e expressão da corrente a corrente conta com uma parte que vamos chamar de (corrente inicial) e outra parte que vamos chamar de (corrente final). A expressão para a corrente então é a parte fixa (corrente final) somada com a parte que varia no tempo (soma da corrente inicial e final). Vamos escrever para ficar mais claro:
Calcular é simples, basta fechar a chave e considerar que o indutor é um curto circuito. Assim temos:
A corrente é a que já está no circuito (3mA), bastando substituir na equação de agora os valores que conhecemos:
Bora calcular a tensão agora no próximo passo!
Passo 3
Vamos começar escrevendo a expressão de tensão para os indutores:
A tensão quando a chave fecha é facinho de determinar se lembrarmos da lei de ohm. Como o indutor é um curto-circuito a tensão E é a tensão da fonte subtraída da tensão causada pela corrente inicial (V = RI). Vamos calcular para substituir na expressão:
Substituindo e na equação de :
Pronto!
Passo 4
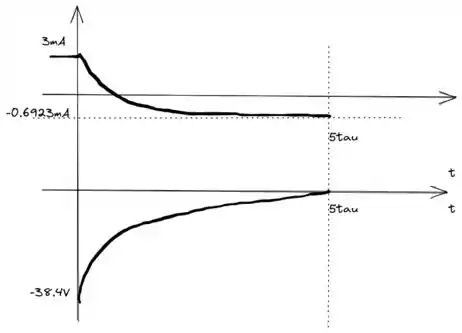
Por último falta só desenhar nosso gráfico. Temos que lembrar que temos uma corrente inicial fixa e uma corrente final que calculamos para representar no esboço:
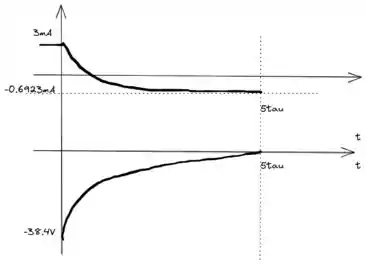
Resposta
a)
b)