Para o circuito da Figura 18.133, determine dois ramos equivalentes aplicando o teorema da substituição a-b.
Passo 1
Falaa galerinhaa!!! Tudo certinhoo?? Bora juntos pra mais uma!!
Aqui, nós temos a opção de fazer o ramo da corrente e o ramo da tensão. Ou seja, teríamos os dois casos de ramo:
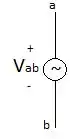
Assim, temos pela corrente:
Substituindo os valores que temos, de Ra = 4 kΩ e Rb = 8 kΩ, e i = 4 mA, então:
Certo, fizemos por um ramo, tendo que Iab = 1,333 mA. Agora vamos fazer pelo caso da tensão.
Passo 2
Temos aqui, que:
Substituindo os valores, temos
Prontinho, encontramos o valor da tensão entre os terminais a e b. Como temos pela fórmula de ohm, a tensão é dependente da corrente e da resistência em questão. Por isso, primeiro obtivemos o valor de Iab, para assim, conseguirmos chegar em Vab. E prontinho, galera!! Resolvemos mais essa. Bora pra próxima
Resposta