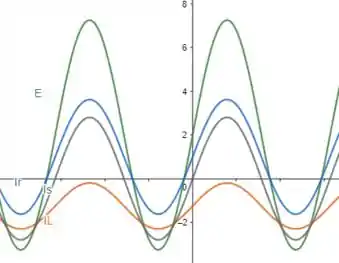
Para o circuito da figura 15.136:
a) Determine a admitância total em forma polar
b) Construa o diagrama de admitâncias
c) Determine a tensão e as correntes e na forma fasorial
d) Construa o diagrama de fasores para as correntes e e a tensão
e) Confirme a validade da lei de Kirchhoff para correntes em um dos nós
f) Calcule a potência média fornecida ao circuito
g) Calcule o fator de potência do circuito e indique se ele é atrasado ou adiantado
h) Determine as expressões senoidais para as correntes e para a tensão sendo a frequência
i) Plote as formas de onda para as correntes e para a tensão no mesmo gráfico
Passo 1
Oiii gente, tudo certinho? Vamos lá pra mais um exercício 😊
a) No nosso circuito, temos um resistor em paralelo com um indutor
O resistor é visto apenas com a parte real de , ou seja
Enquanto o indutor é visto só com a parte imaginária positiva:
Nesse caso, a impedância equivalente em paralelo é dada assim:
Como a admitância é o inverso da impedância, temos
Escrevendo na forma retangular:
E, voltando pra forma polar hahahaa:
Passo 2
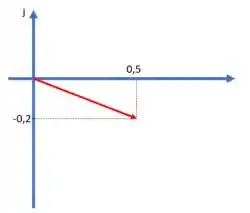
b) Sabendo que , o diagrama de admitâncias fica assim:
Passo 3
c) Vamos lá, pra encontrarmos a tensão , vamos fazer
Pela imagem do circuito, temos que , e o nós encontramos no item a, ele vale
Então
Passo 4
Agora para encontrarmos , vamos fazer
Substituindo os valores:
Passo 5
E por fimmm, vamos encontrar :
Substituindo:
Então
Passo 6
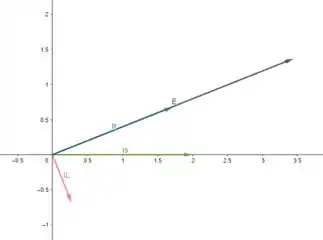
d) Certo, agora queremos o diagrama de fasores para as correntes e para a tensão
Basicamente, temos que colocar no plano complexo aquilo que achamos no item anterior, mas antes vamos colocar tudo na forma retangular:
Opa, então colocando tudo isso no plano complexo, temos
Passo 7
e) Vamos confirmar a Lei de Kirchhoff das correntes no nó superior do circuito
Ali, está entrando e saindo e , então temos que ter
A parte imaginária some e só nos resta:
Logo, está confirmado a LKI hahahaha essa aproximação acontece porque lá em cima a gente arredondou algumas coisas
Passo 8
f) A potência média fornecida ao circuito é
Então:
Passo 9
g) O fator de potência é calculado assim:
Como , temos que
Além disso, conforme encontramos no item a, o módulo de é , então
Que é um fator de potência atrasado :)
Passo 10
h) Vamos lá, começando pela tensão. Sua forma senoidal é dada assim:
Onde
Então, substituindo os valores:
(esse e é pra gente converter pra radianos, já que a frequência está em rad/s okkk?)
Boaaa, agora é só fazer o mesmo pras correntes
Passo 11
Para , temos
Para :
E por fim, para :
Passo 12
i) Agora é só a gente plotar as formas senoidais do item anterior, isso vai nos dar:
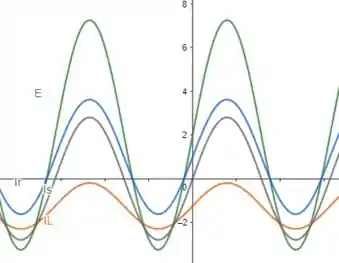
E acabamoooos :D
Resposta
a)
b) 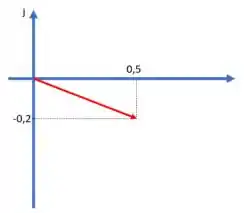
c)
d) 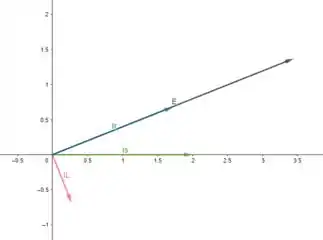
f)
g) atrasado
h)
i)