Para o circuito da Figura :
- Determine a admitância total em forma polar.
- Construa o diagrama de admitâncias.
- Calcule o valor de em microfarads e o de em henries.
- Determine a tensão e as correntes e em forma fasorial.
- Construa o diagrama de fasores para as correntes , , e a tensão .
- Confirme a lei de Kirchhoff para correntes em um dos nós.
- Calcule a potência média fornecida ao circuito.
- Calcule o fator de potência e indique se ele é atraso ou adiantado.
- Determine expressões senoidais para as correntes e para a tensão.
- Plote as formas de onda da tensão e das correntes no mesmo gráfico.
Passo 1
Opa pessoal, tudo certinho aí? Vamos resolver esta questão.
Analisando a figura , temos os seguintes dados:
Escrevendo estes dados na forma polar temos que:
A admitância é dada por:
Portanto:
Resolvendo, temos que:
Passo 2
Podemos então desenhar um esboço de como ficaria o diagrama de admitância:
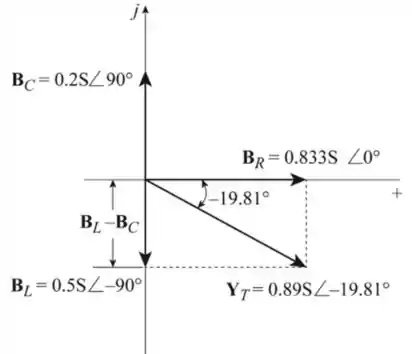
Passo 3
Para o item (c), temos que:
Como a frequência de trabalho é de , temos que:
Substituindo os dados, temos que:
E:
Passo 4
A tensão é dada por:
Substituindo os valores, temos que:
Para temos:
Substituindo os valores, temos que:
Portanto:
Para temos que:
Substituindo os valores, temos que:
Portanto:
Para temos que:
Substituindo os valores, temos que:
Portanto:
Passo 5
Temos então o seguinte diagrama de fasores:
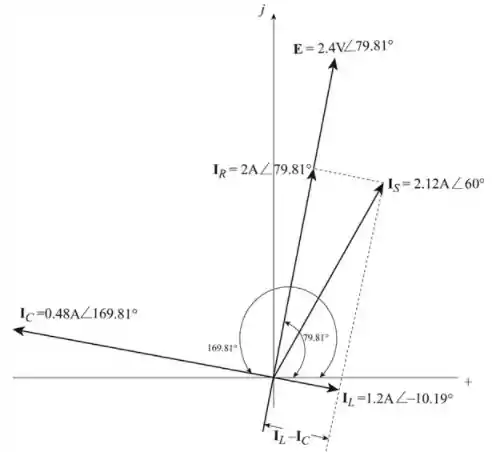
Passo 6
Aplicando a lei de Kirchhoff ao nó, temos que:
Substituindo os valores, temos que:
Resolvendo, temos que:
Portanto, a lei de Kirchhoff é válida.
Passo 7
Para a potência média fornecida ao circuito, temos que:
Substituindo os valores e calculando, temos que:
Passo 8
Para calcular o fator de potência do circuito, temos que:
Substituindo os valores e calculando, temos que:
Passo 9
No item (h) queremos as expressões senoidais para as correntes e para a tensão dada uma frequência de .
Para a tensão, temos que:
E para a corrente, temos que:
Onde indica o valor do pico de tensão e pico de corrente.
Temos também que:
Portanto:
E:
Para , temos que:
E para , temos que:
Passo 10
O item (i) nos pede para plotar o diagrama com as equações do item anterior. Temos o seguinte esboço:
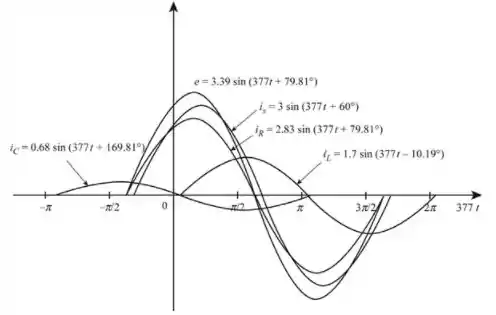
Resposta
- Imagem .
- Imagem .
- A lei de Kirchhoff é válida.
- .
- Imagem .